Chapter 7 图

图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。

图定义

图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。

对于图的定义，我们需要明确几个注意的地方。
线性表中我们把数据元素叫元素，树中将数据元素叫结点，在图中数据元素，我们则称之为顶点（Vertex）。
线性表中可以没有数据元素，称为空表。树中可以没有结点，叫做空树。在图结构中，不允许没有顶点。在定义中，若V是顶点的集合，则强调了顶点集合V有穷非空。
线性表中，相邻的数据元素之间具有线性关系，树结构中，相邻两层的结点具有层次关系，而图中，任意两个顶点之间都可能有关系，顶点之间的逻辑关系用边来表示，边集可以是空的。

各种图定义

无向边

若顶点vi到vj之间的边没有方向，则称这条边为无向边（Edge），用无序偶对(vi,vj)来表示。
如果图中任意两个顶点之间的边都是无向边，则称该图为无向图。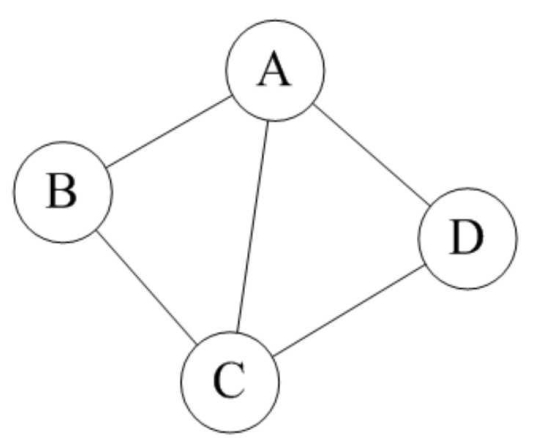

上图就是一个无向图，由于是无方向的，连接顶点A与D的边，可以表示成无序对(A,D)，也可以写成(D,A)。
对于图中的无向图G1来说，G1=(V1,{E1})，其中顶点集合V1={A,B,C,D}；边集合E1={(A,B),(B,C),(C,D),(D,A),(A,C)}

在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。含有n个顶点的无向完全图有n(n-1)/2条边。

有向边

若从顶点vi到vj的边有方向，则称这条边为有向边，也称为弧（Arc）。
用有序偶<vi,vj>来表示，vi称为弧尾（Tail），vj称为弧头（Head）。
如果图中任意两个顶点之间的边都是有向边，则称该图为有向图（Directed graphs）。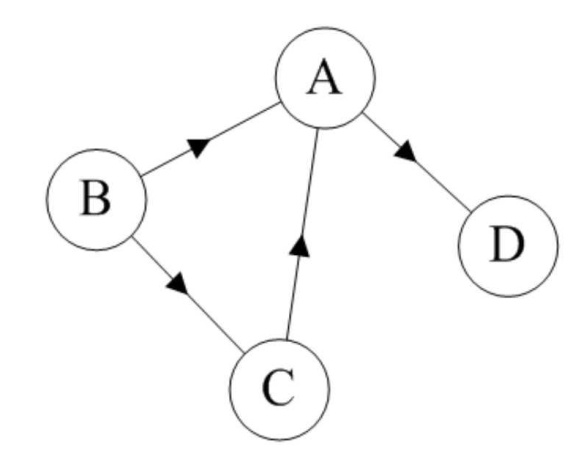

上图就是一个有向图。连接顶点A到D的有向边就是弧，A是弧尾，D是弧头，<A,D>表示弧，注意不能写成<D,A>。
对于图中的有向图G2来说，G2=(V2,{E2})，其中顶点集合V2={A,B,C,D}；弧集合E2={<A,D>,<B,A>,<C,A>,<B,C>}。
无向边用小括号“()”表示，而有向边则是用尖括号“<>”表示。
在图中，若不存在顶点到其自身的边，且同一条边不重复出现，则称这样的图为简单图。

在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则称该图为有向完全图。含有n个顶点的有向完全图有n×(n-1)条边。
从这里也可以得到结论，对于具有n个顶点和e条边数的图，无向图0≤e≤n(n-1)/2，有向图0≤e≤n(n-1)。

有些图的边或弧具有与它相关的数字，这种与图的边或弧相关的数叫做权（Weight）。这些权可以表示从一个顶点到另一个顶点的距离或耗费。这种带权的图通常称为网（Network）。

假设有两个图G=(V,{E})和G’=(V’,{E’})，如果V’V且E’E，则称G’为G的子图（Sub-graph）。例如图，带底纹的图均为左侧无向图与有向图的子图。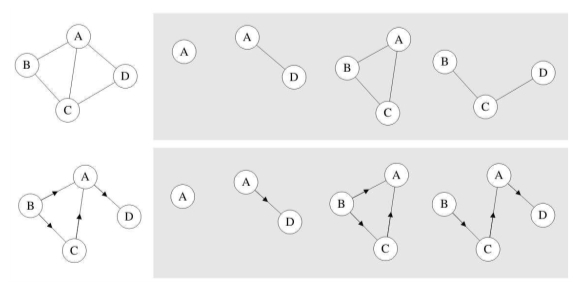

图的顶点与边间关系

对于无向图G=(V,{E})，如果边(v,v’)∈E，则称顶点v和v’互为邻接点（Adjacent），即v和v’相邻接。
边(v,v’)依附（incident）于顶点v和v’，或者说(v,v’)与顶点v和v’相关联。
顶点v的度（Degree）是和v相关联的边的数目，记为TD(v)。


例如图左侧上方的无向图，顶点A与B互为邻接点，边(A,B)依附于顶点A与B上，顶点A的度为3。而此图的边数是5，各个顶点度的和=3+2+3+2=10，推敲后发现，边数其实就是各顶点度数和的一半，多出的一半是因为重复两次记数。

对于有向图G=(V,{E})，如果弧<v,v’>∈E，则称顶点v邻接到顶点v’，顶点v’邻接自顶点v。弧<v,v’>和顶点v，v’相关联。以顶点v为头的弧的数目称为v的入度（InDegree），记为ID(v)；以v为尾的弧的数目称为v的出度（OutDegree），记为OD(v)；顶点v的度为TD(v)=ID(v)+OD(v)。

无向图G=(V,{E})中从顶点v到顶点v’的路径（Path）是一个顶点序列(v=vi,0,vi,1,…,vi,m=v’)，其中(vi,j-1,vi,j)∈E，1≤j≤m。例如图中就列举了顶点B到顶点D四种不同的路径。
如果G是有向图，则路径也是有向的，顶点序列应满足<vi,j-1,vi,j>∈E，1≤j≤m。

第一个顶点和最后一个顶点相同的路径称为回路或环（Cycle）。序列中顶点不重复出现的路径称为简单路径。除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路，称为简单回路或简单环。

连通图相关术语

在无向图G中，如果从顶点v到顶点v’有路径，则称v和v’是连通的。如果对于图中任意两个顶点vi、vj∈V，vi和vj都是连通的，则称G是连通图（Connected Graph）。

无向图中的极大连通子图称为连通分量。注意连通分量的概念，它强调：
要是子图；
子图要是连通的；
连通子图含有极大顶点数；
具有极大顶点数的连通子图包含依附于这些顶点的所有边。

在有向图G中，如果对于每一对vi、vj∈V、vi≠vj，从vi到vj和从vj到vi都存在路径，则称G是强连通图。有向图中的极大强连通子图称做有向图的强连通分量。

所谓的一个连通图的生成树是一个极小的连通子图，它含有图中全部的n个顶点，但只有足以构成一棵树的n-1条边。
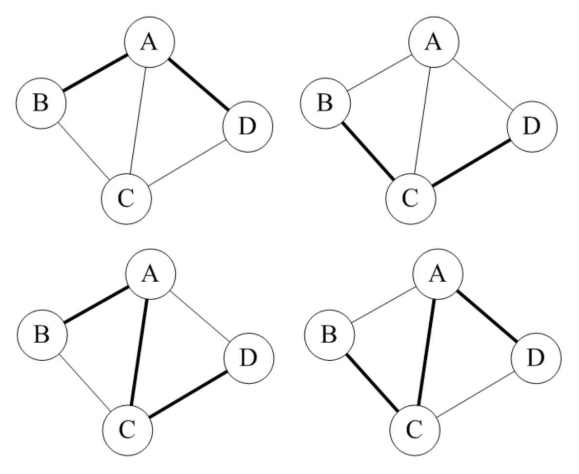
比如图的图1是一普通图，但显然它不是生成树，当去掉两条构成环的边后，比如图2或图3，就满足n个顶点n-1条边且连通的定义了。它们都是一棵生成树。
从这里也可知道，如果一个图有n个顶点和小于n-1条边，则是非连通图，如果它多于n-1边条，必定构成一个环，因为这条边使得它依附的那两个顶点之间有了第二条路径。
比如图2和图3，随便加哪两顶点的边都将构成环。不过有n-1条边并不一定是生成树，比如图4。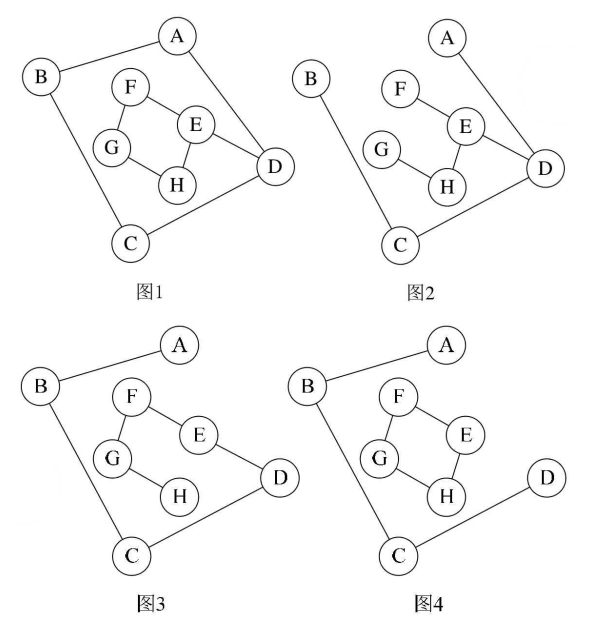

如果一个有向图恰有一个顶点的入度为0，其余顶点的入度均为1，则是一个有向树。
对有向树的理解比较容易，所谓入度为0其实就相当于树中的根结点，其余顶点入度为1就是说树的非根结点的双亲只有一个。
一个有向图的生成森林由若干棵有向树组成，含有图中全部顶点，但只有足以构成若干棵不相交的有向树的弧。
如图的图1是一棵有向图。去掉一些弧后，它可以分解为两棵有向树，如图2和图3，这两棵就是图1有向图的生成森林。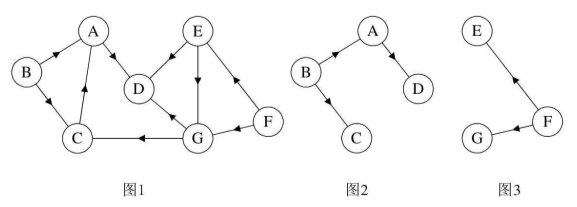

图的定义与术语总结

图按照有无方向分为无向图和有向图。无向图由顶点和边构成，有向图由顶点和弧构成。弧有弧尾和弧头之分。

图按照边或弧的多少分稀疏图和稠密图。如果任意两个顶点之间都存在边叫完全图，有向的叫有向完全图。若无重复的边或顶点到自身的边则叫简单图。

图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫做度，有向图顶点分为入度和出度。

图上的边或弧上带权则称为网。

图中顶点间存在路径，两顶点存在路径则说明是连通的，如果路径最终回到起始点则称为环，当中不重复叫简单路径。
若任意两顶点都是连通的，则图就是连通图，有向则称强连通图。
图中有子图，若子图极大连通则就是连通分量，有向的则称强连通分量。

无向图中连通且n个顶点n-1条边叫生成树。有向图中一顶点入度为0其余顶点入度为1的叫有向树。一个有向图由若干棵有向树构成生成森林。

图的抽象数据类型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
ADT  图(Graph)
	Data
		顶点的有穷非空集合和边的集合。
	Operation
		CreateGraph(*G,  V,  VR):  按照顶点集V和边弧集VR的定义构造图G。
		DestroyGraph(*G):          图G存在则销毁。
		LocateVex(G,  u):          若图G中存在顶点u，则返回图中的位置。
		GetVex(G,  v):             返回图G中顶点v的值。
		PutVex(G,  v,  value):     将图G中顶点v赋值value。
		FirstAdjVex(G,  *v):       返回顶点v的一个邻接顶点，若顶点在G中无邻接顶点返回空。
		NextAdjVex(G,  v,  *w):    返回顶点v相对于顶点w的下一个邻接顶点，若w是v的最后一个邻接点则返回“空”。
		InsertVex(*G,  v):         在图G中增添新顶点v。
		DeleteVex(*G,  v):         删除图G中顶点v及其相关的弧。
		InsertArc(*G,  v,  w):     在图G中增添弧<v,w>，若G是无向图，还需要增添对称弧<w,v>。
		DeleteArc(*G,  v,  w):     在图G中删除弧<v,w>，若G是无向图，则还删除对称弧<w,v>。
		DFSTraverse(G):            对图G中进行深度优先遍历，在遍历过程对每个顶点调用。
		HFSTraverse(G):            对图G中进行广度优先遍历，在遍历过程对每个顶点调用。
endADT

图的存储结构

由于图的结构比较复杂，任意两个顶点之间都可能存在联系，因此无法以数据元素在内存中的物理位置来表示元素之间的关系，也就是说，图不可能用简单的顺序存储结构来表示。
而多重链表的方式，即以一个数据域和多个指针域组成的结点表示图中的一个顶点，尽管可以实现图结构，但其实在树中，我们也已经讨论过，这是有问题的。
如果各个顶点的度数相差很大，按度数最大的顶点设计结点结构会造成很多存储单元的浪费，而若按每个顶点自己的度数设计不同的顶点结构，又带来操作的不便。
因此，对于图来说，如何对它实现物理存储是个难题，不过我们的前辈们已经解决了，现在我们来看前辈们提供的五种不同的存储结构。

邻接矩阵

考虑到图是由顶点和边或弧两部分组成。
合在一起比较困难，那就很自然地考虑到分两个结构来分别存储。
顶点不分大小、主次，所以用一个一维数组来存储是很不错的选择。
而边或弧由于是顶点与顶点之间的关系，一维搞不定，那就考虑用一个二维数组来存储。
于是我们的邻接矩阵的方案就诞生了。

图的邻接矩阵（Adjacency Matrix）存储方式是用两个数组来表示图。
一个一维数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中的边或弧的信息。

设图G有n个顶点，则邻接矩阵是一个n×n的方阵，定义为：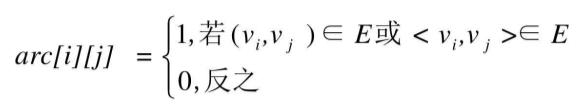

我们来看一个实例，左图就是一个无向图。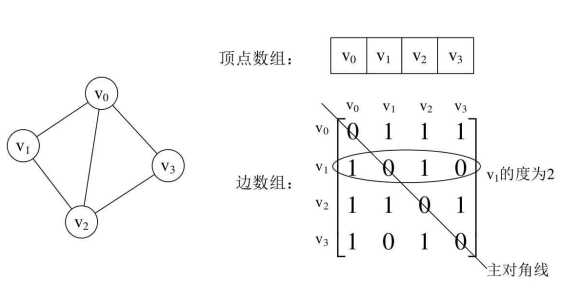

我们可以设置两个数组，顶点数组为ver-tex[4]={v0,v1,v2,v3}，边数组arc[4][4]为右图这样的一个矩阵。
简单解释一下，对于矩阵的主对角线的值，即arc[0][0]、arc[1][1]、arc[2][2]、arc[3][3]，全为0是因为不存在顶点到自身的边，比如v0到v0。
arc[0][1]=1是因为v0到v1的边存在，而arc[1][3]=0是因为v1到v3的边不存在。
并且由于是无向图，v1到v3的边不存在，意味着v3到v1的边也不存在。所以无向图的边数组是一个对称矩阵。

有了这个矩阵，我们就可以很容易地知道图中的信息。
1.我们要判定任意两顶点是否有边无边就非常容易了。
2.我们要知道某个顶点的度，其实就是这个顶点vi在邻接矩阵中第i行（或第i列）的元素之和。比如顶点v1的度就是1+0+1+0=2。
3.求顶点vi的所有邻接点就是将矩阵中第i行元素扫描一遍，arc[i][j]为1就是邻接点。

我们再来看一个有向图样例，如图所示的左图。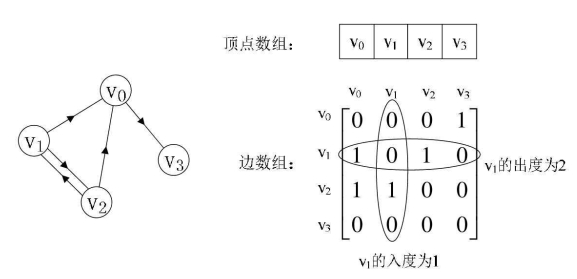

顶点数组为vertex[4]={v0,v1,v2,v3}，弧数组arc[4][4]为右图这样的一个矩阵。主对角线上数值依然为0。
但因为是有向图，所以此矩阵并不对称，比如由v1到v0有弧，得到arc[1][0]=1，而v0到v1没有弧，因此arc[0][1]=0。

有向图讲究入度与出度，顶点v1的入度为1，正好是第v1列各数之和。顶点v1的出度为2，即第v1行的各数之和。

与无向图同样的办法，判断顶点vi到vj是否存在弧，只需要查找矩阵中arc[i][j]是否为1即可。
要求vi的所有邻接点就是将矩阵第i行元素扫描一遍，查找arc[i][j]为1的顶点。

在图的术语中，我们提到了网的概念，也就是每条边上带有权的图叫做网。那么这些权值就需要存下来，如何处理这个矩阵来适应这个需求呢？我们有办法。

设图G是网图，有n个顶点，则邻接矩阵是一个n×n的方阵，定义为：这里wij表示（vi,vj）或<vi,vj>上的权值。
∞表示一个计算机允许的、大于所有边上权值的值，也就是一个不可能的极限值。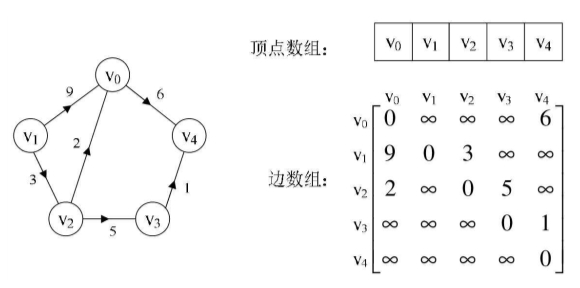

那么邻接矩阵是如何实现图的创建的呢？我们先来看看图的邻接矩阵存储的结构，代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/*  顶点类型应由用户定义  */
typedef  char  VertexType;                          
/*  边上的权值类型应由用户定义  */
typedef  int  EdgeType;                                
/*  最大顶点数，应由用户定义  */
#define  MAXVEX  100                                      
/*  用65535来代表∞  */
#define  INFINITY  65535
typedef  struct
{
	/*  顶点表  */
	VertexType  vexs[MAXVEX];                  
	/*  邻接矩阵，可看作边表  */
	EdgeType  arc[MAXVEX][MAXVEX];        
	/*  图中当前的顶点数和边数  */
	int  numVertexes,  numEdges;              
}  MGraph;

有了这个结构定义，我们构造一个图，其实就是给顶点表和边表输入数据的过程。我们来看看无向网图的创建代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/*  建立无向网图的邻接矩阵表示  */
void  CreateMGraph(MGraph  *G)
{
	int  i,  j,  k,  w;
	printf("输入顶点数和边数:\n");

	/*  输入顶点数和边数  */
	scanf("%d,%d",  &G->numVertexes,  &G->numEdges);

    /*  读入顶点信息，建立顶点表  */
	for  (i  =  0;  i  <  G->numVertexes;  i++)                       scanf(&G->vexs[i]);
	for  (i  =  0;  i  <  G->numVertexes;  i++)	for  (j  =  0;  j  <G->numVertexes;  j++) /*  邻接矩阵初始化  */	G->arc[i][j]  =  INFINITY;  
    /*  读入numEdges条边，建立邻接矩阵  */
	for  (k  =  0;  k  <  G->numEdges;  k++)
    {
		printf("输入边(vi,vj)上的下标i，下标j和权w:\n");
		/*  输入边(vi,vj)上的权w  */
		scanf("%d,%d,%d",  &i,  &j,  &w); 
		G->arc[i][j]  =  w;
		/*  因为是无向图，矩阵对称  */
		G->arc[j][i]  =  G->arc[i][j];                                    
	}
}

从代码中也可以得到，n个顶点和e条边的无向网图的创建，时间复杂度为O(n+n2+e)，其中对邻接矩阵G.arc的初始化耗费了O(n2)的时间。

邻接表

邻接矩阵是不错的一种图存储结构，但是我们也发现，对于边数相对顶点较少的图，这种结构是存在对存储空间的极大浪费的。

因此我们考虑另外一种存储结构方式。回忆我们在线性表时谈到，顺序存储结构就存在预先分配内存可能造成存储空间浪费的问题，于是引出了链式存储的结构。同样的，我们也可以考虑对边或弧使用链式存储的方式来避免空间浪费的问题。

再回忆我们在树中谈存储结构时，讲到了一种孩子表示法，将结点存入数组，并对结点的孩子进行链式存储，不管有多少孩子，也不会存在空间浪费问题。这个思路同样适用于图的存储。我们把这种数组与链表相结合的存储方法称为邻接表（Ad-jacency List）。

邻接表的处理办法是这样。
1.图中顶点用一个一维数组存储，当然，顶点也可以用单链表来存储，不过数组可以较容易地读取顶点信息，更加方便。
另外，对于顶点数组中，每个数据元素还需要存储指向第一个邻接点的指针，以便于查找该顶点的边信息。
2.图中每个顶点vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以用单链表存储，无向图称为顶点vi的边表，有向图则称为顶点vi作为弧尾的出边表。

例如图所示的就是一个无向图的邻接表结构。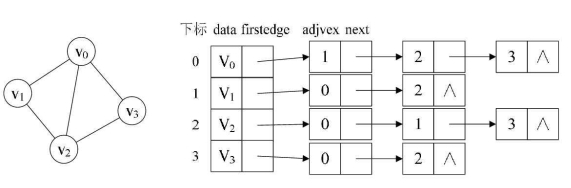

从图中我们知道，顶点表的各个结点由data和firstedge两个域表示，data是数据域，存储顶点的信息，firstedge是指针域，指向边表的第一个结点，即此顶点的第一个邻接点。
边表结点由adjvex和next两个域组成。adjvex是邻接点域，存储某顶点的邻接点在顶点表中的下标，next则存储指向边表中下一个结点的指针。
比如v1顶点与v0、v2互为邻接点，则在v1的边表中，adjvex分别为v0的0和v2的2。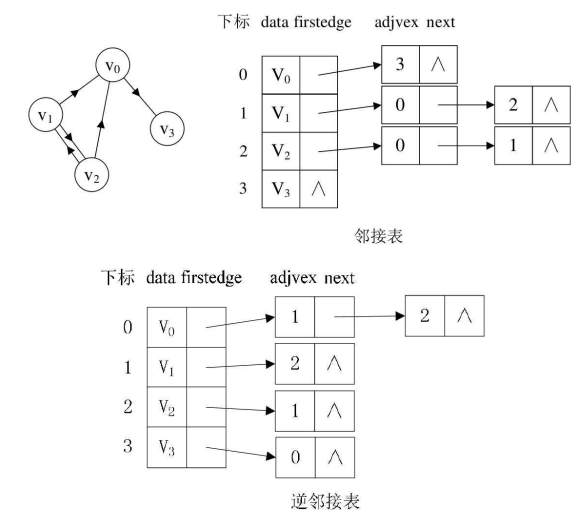

有了这些结构的图，下面关于结点定义的代码就很好理解了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/*  顶点类型应由用户定义  */
typedef  char  VertexType;                    
/*  边上的权值类型应由用户定义  */
typedef  int  EdgeType; 
                         
/*  边表结点  */
typedef  struct  EdgeNode                      
{
	/*  邻接点域，存储该顶点对应的下标  */
	int  adjvex;                                      
	/*  用于存储权值，对于非网图可以不需要  */
	EdgeType  weight;                            
	/*  链域，指向下一个邻接点　  */
	struct  EdgeNode  *next;                
}  EdgeNode;

/*  顶点表结点  */
typedef  struct  VertexNode                  
{
	/*  顶点域，存储顶点信息  */
	VertexType  data;                            
	/*  边表头指针  */EdgeNode  *firstedge;                    
}  VertexNode,  AdjList[MAXVEX];

typedef  struct{
	AdjList  adjList;
	/*  图中当前顶点数和边数  */
	int  numVertexes,  numEdges;        
}  GraphAdjList;

无向图的邻接表创建代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/*  建立图的邻接表结构  */
void    CreateALGraph(GraphAdjList  *G)
{
	int  i,  j,  k;
	EdgeNode  *e;
	printf("输入顶点数和边数:\n");
	/*  输入顶点数和边数  */
	scanf("%d,%d",  &G->numVertexes,  &G->numEdges);       
	/*  读入顶点信息，建立顶点表  */
	for  (i  =  0;  i  <  G->numVertexes;  i++)                       
	{
		/*  输入顶点信息  */
		scanf(&G->adjList[i].data);                                      
		/*  将边表置为空表  */
		G->adjList[i].firstedge  =  NULL;                              
	}
	/*  建立边表  */
	for  (k  =  0;  k  <  G->numEdges;  k++)                          
	{
		printf("输入边(vi,vj)上的顶点序号:\n");
		/*  输入边(vi,vj)上的顶点序号  */
		scanf("%d,%d",  &i,  &j);
       	/*  向内存申请空间，  */
		/*  生成边表结点  */
		e  =  (EdgeNode  *)malloc(sizeof(EdgeNode));          
		/*  邻接序号为j  */
		e->adjvex  =  j;                                                  
		/*  将e指针指向当前顶点指向的结点  */
		e->next  =  G->adjList[i].firstedge; 
		/*  将当前顶点的指针指向e  */
		G->adjList[i].firstedge  =  e;                                    
		/*  向内存申请空间，  */
	}
}  

本算法的时间复杂度，对于n个顶点e条边来说，很容易得出是O(n+e)。

十字链表

那么对于有向图来说，邻接表是有缺陷的。
关心了出度问题，想了解入度就必须要遍历整个图才能知道，反之，逆邻接表解决了入度却不了解出度的情况。
有没有可能把邻接表与逆邻接表结合起来呢？答案是肯定的，就是把它们整合在一起。
这就是我们现在要讲的有向图的一种存储方法：十字链表（Orthogonal List）。

我们重新定义顶点表结点结构如表所示。
data firstin firstout
其中firstin表示入边表头指针，指向该顶点的入边表中第一个结点，firstout表示出边表头指针，指向该顶点的出边表中的第一个结点。

重新定义的边表结点结构如表所示。
tailvex headvex headlink taillink
其中tailvex是指弧起点在顶点表的下标，headvex是指弧终点在顶点表中的下标，headlink是指入边表指针域，指向终点相同的下一条边，taillink是指边表指针域，指向起点相同的下一条边。
如果是网，还可以再增加一个weight域来存储权值。


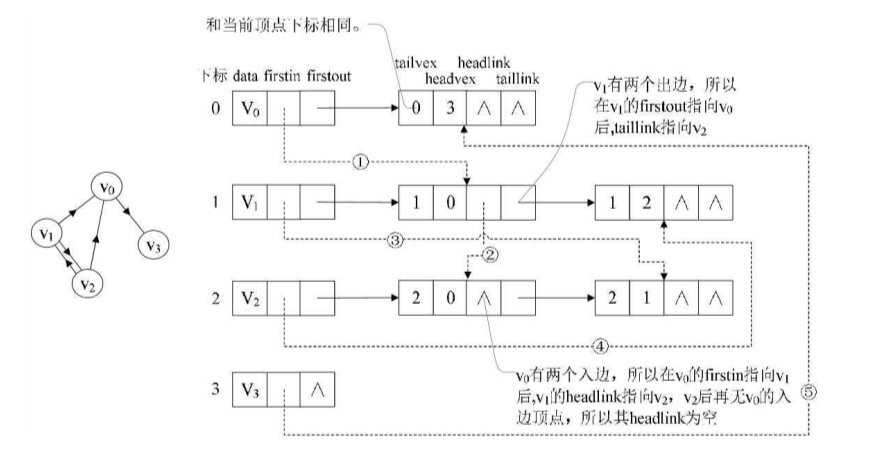
如图，顶点依然是存入一个一维数组{v0,v1,v2,v3}。
就以顶点v0来说，firstout指向的是出边表中的第一个结点v3。所以v0边表结点的headvex=3，而tailvex其实就是当前顶点v0的下标0，由于v0只有一个出边顶点，所以headlink和taillink都是空。

我们重点需要来解释虚线箭头的含义，它其实就是此图的逆邻接表的表示。
对于v0来说，它有两个顶点v1和v2的入边。因此v0的firstin指向顶点v1的边表结点中headvex为0的结点，如图7-4-10右图中的①。
接着由入边结点的headlink指向下一个入边顶点v2，如图中的②。
对于顶点v1，它有一个入边顶点v2，所以它的firstin指向顶点v2的边表结点中headvex为1的结点，如图中的③。
顶点v2和v3也是同样有一个入边顶点，如图中④和⑤。

十字链表的好处就是因为把邻接表和逆邻接表整合在了一起，这样既容易找到以vi为尾的弧，也容易找到以vi为头的弧，因而容易求得顶点的出度和入度。
而且它除了结构复杂一点外，其实创建图算法的时间复杂度是和邻接表相同的，因此，在有向图的应用中，十字链表是非常好的数据结构模型。

邻接多重表

讲了有向图的优化存储结构，对于无向图的邻接表，有没有问题呢？
如果我们在无向图的应用中，关注的重点是顶点，那么邻接表是不错的选择，但如果我们更关注边的操作，比如对已访问过的边做标记，删除某一条边等操作，那就意味着，需要找到这条边的两个边表结点进行操作，这其实还是比较麻烦的。
比如图，若要删除左图的(v0,v2)这条边，需要对邻接表结构中右边表的阴影两个结点进行删除操作，显然这是比较烦琐的。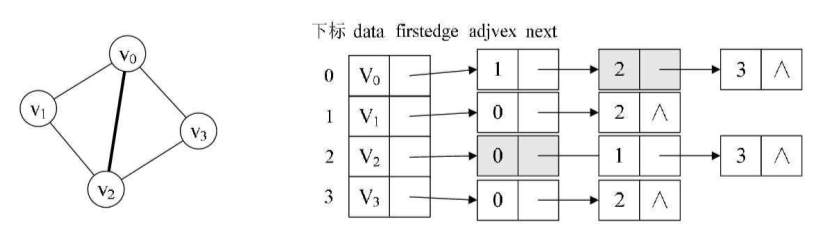

因此，我们也仿照十字链表的方式，对边表结点的结构进行一些改造，也许就可以避免刚才提到的问题。
重新定义的边表结点结构如下所示。
ivex ilink jvex jlink
其中ivex和jvex是与某条边依附的两个顶点在顶点表中的下标。
ilink指向依附顶点ivex的下一条边，jlink指向依附顶点jvex的下一条边。
这就是邻接多重表结构。

我们来看结构示意图的绘制过程，理解了它是如何连线的，也就理解邻接多重表构造原理了。
如图所示，左图告诉我们它有4个顶点和5条边，显然，我们就应该先将4个顶点和5条边的边表结点画出来。
由于是无向图，所以ivex是0、jvex是1还是反过来都是无所谓的，不过为了绘图方便，都将ivex值设置得与一旁的顶点下标相同。

我们开始连线，如图所示。
首先连线的①②③④就是将顶点的firstedge指向一条边，顶点下标要与ivex的值相同，这很好理解。
接着，由于顶点v0的(v0,v1)边的邻边有(v0,v3)和(v0,v2)。因此⑤⑥的连线就是满足指向下一条依附于顶点v0的边的目标，注意ilink指向的结点的jvex一定要和它本身的ivex的值相同。
同样的道理，连线⑦就是指(v1,v0)这条边，它是相当于顶点v1指向(v1,v2)边后的下一条。
v2有三条边依附，所以在③之后就有了⑧⑨。
连线⑩的就是顶点v3在连线④之后的下一条边。
左图一共有5条边，所以右图有10条连线，完全符合预期。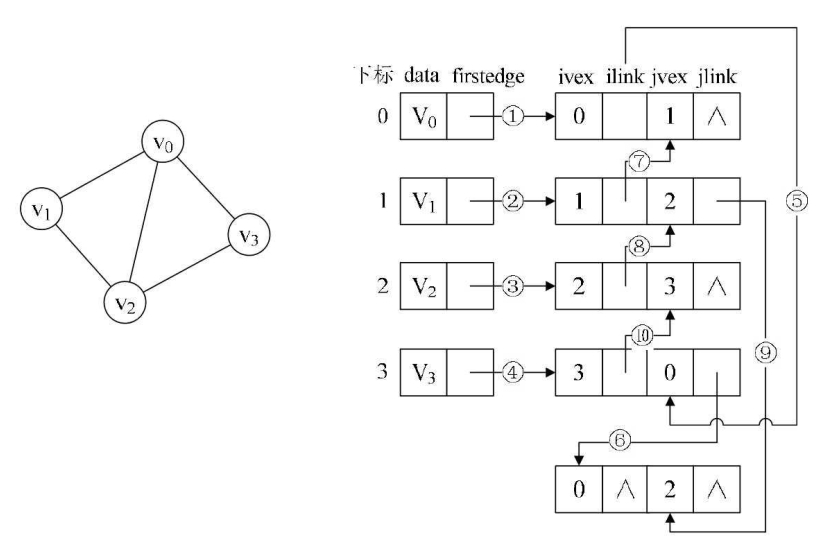

到这里，大家应该可以明白，邻接多重表与邻接表的差别，仅仅是在于同一条边在邻接表中用两个结点表示，而在邻接多重表中只有一个结点。
这样对边的操作就方便多了，若要删除左图的(v0,v2)这条边，只需要将图中的⑥⑨的链接指向改为∧即可。

边集数组

边集数组是由两个一维数组构成。
一个是存储顶点的信息；另一个是存储边的信息，这个边数组每个数据元素由一条边的起点下标（begin）、终点下标（end）和权（weight）组成，如图所示。
显然边集数组关注的是边的集合，在边集数组中要查找一个顶点的度需要扫描整个边数组，效率并不高。
因此它更适合对边依次进行处理的操作，而不适合对顶点相关的操作。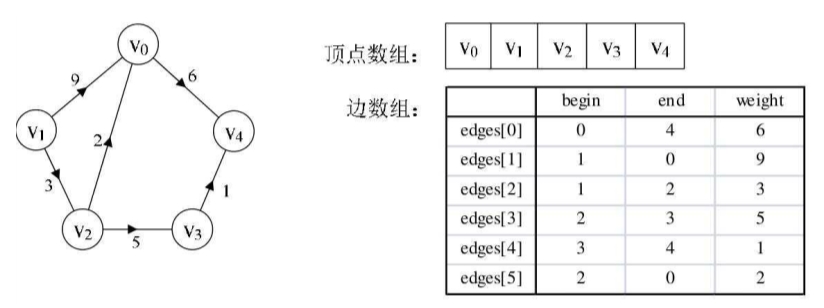

图的遍历

深度优先遍历

深度优先遍历（Depth_First_Search），也有称为深度优先搜索，简称为DFS。

如果我们用的是邻接矩阵的方式，则代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/*  Boolean是布尔类型，其值是TRUE或FALSE  */
typedef  int  Boolean;                         
/*  访问标志的数组  */
Boolean  visited[MAX];
                        
/*  邻接矩阵的深度优先递归算法  */
void  DFS(MGraph  G,  int  i)
{
	int  j;
	visited[i]  =  TRUE;

	/*  打印顶点，也可以其他操作  */
	printf("%c  ",  G.vexs[i]);  
      
	for  (j  =  0;  j  <  G.numVertexes;  j++)
	{
		if  (G.arc[i][j]  ==  1  &&  !visited[j])
		{
			/*  对为访问的邻接顶点递归调用  */
			DFS(G,  j);
		}
	}                      
}

/*  邻接矩阵的深度遍历操作  */
void  DFSTraverse(MGraph  G)
{
	int  i;
	for  (i  =  0;  i  <  G.numVertexes;  i++)
	{
		/*  初始所有顶点状态都是未访问过状态  */visited[i]  =  FALSE; 
	}           
	for  (i  =  0;  i  <  G.numVertexes;  i++)
	{
		/*  对未访问过的顶点调用DFS，若是连通图，只会执行一次  */
		if  (!visited[i])
		{
			 DFS(G,  i);
		}                 
	}
}

如果图结构是邻接表结构，其DFSTraverse函数的代码是几乎相同的，只是在递归函数中因为将数组换成了链表而有不同，代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/*  邻接表的深度优先递归算法  */
void  DFS(GraphAdjList  GL,  int  i)
{
	EdgeNode  *p;
	visited[i]  =  TRUE;

	/*  打印顶点，也可以其他操作  */
	printf("%c  ",  GL->adjList[i].data); 
       
	p  =  GL->adjList[i].firstedge;
	while  (p)
	{
		if  (!visited[p->adjvex])/*  对未访问的邻接顶点递归调用  */
		{
			DFS(GL,  p->adjvex);
		}                        
		p  =  p->next;
	}
}

/*  邻接表的深度遍历操作  */
void  DFSTraverse(GraphAdjList  GL)
{
	int  i;
	for  (i  =  0;  i  <  GL->numVertexes;  i++)
	{
		/*  初始所有顶点状态都是未访问过状态  */
		visited[i]  =  FALSE;
	}                                

	for  (i  =  0;  i  <  GL->numVertexes;  i++)
	{
		/*  对未访问过的顶点调用DFS，若是连通图，只会执行一次  */
		if  (!visited[i])
		{
			DFS(GL,  i);
		}                                      
	}
}

对比两个不同存储结构的深度优先遍历算法，对于n个顶点e条边的图来说，邻接矩阵由于是二维数组，要查找每个顶点的邻接点需要访问矩阵中的所有元素，因此都需要O(n2)的时间。
而邻接表做存储结构时，找邻接点所需的时间取决于顶点和边的数量，所以是O(n+e)。显然对于点多边少的稀疏图来说，邻接表结构使得算法在时间效率上大大提高。

广度优先遍历

广度优先遍历（Breadth_First_Search），又称为广度优先搜索，简称BFS。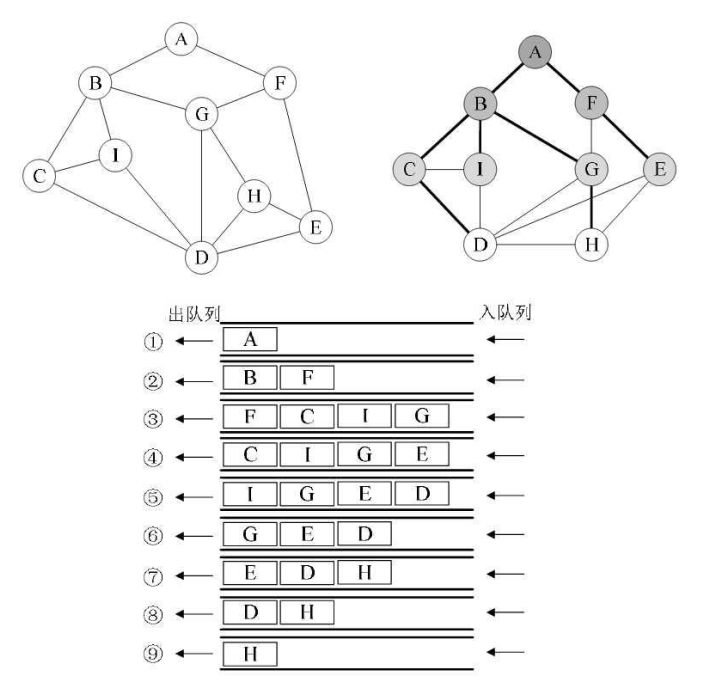

以下是邻接矩阵结构的广度优先遍历算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
/*  邻接矩阵的广度遍历算法  */
void  BFSTraverse(MGraph  G)
{
	int  i,  j;
	Queue  Q;
	for  (i  =  0;  i  <  G.numVertexes;  i++)
	{
		visited[i]  =  FALSE;
	}

	/*  初始化一辅助用的队列  */
	InitQueue(&Q);

	/*  对每一个顶点做循环  */
	for  (i  =  0;  i  <  G.numVertexes;  i++)                            
	{
		/*  若是未访问过就处理  */
		if  (!visited[i])
		{
			/*  设置当前顶点访问过  */
			visited[i]=TRUE;                                                  
			/*  打印顶点，也可以其他操作  */
			printf("%c  ",  G.vexs[i]);                                
			/*  将此顶点入队列  */
			EnQueue(&Q,i);                                                      
			/*  若当前队列不为空  */
			while  (!QueueEmpty(Q))                                      
			{
				/*  将队中元素出队列，赋值给i  */
				DeQueue(&Q,  &i);                                          
				for  (j  =  0;  j  <  G.numVertexes;  j++)
				{
					/*  判断其他顶点若与当前顶点存在边且未访问过  */
					if  (G.arc[i][j]  ==  1  &&  !visited[j])
					{
						/*  将找到的此顶点标记为已访问  */
						visited[j]=TRUE;                          
						/*  打印顶点  */
						printf("%c  ",  G.vexs[j]);        
						/*  将找到的此顶点入队列  */
						EnQueue(&Q,j); 
					}
				}
			}
		} 
	}
}   
```		
对于邻接表的广度优先遍历，代码与邻接矩阵差异不大，代码如下。
```c
/*  邻接表的广度遍历算法  */
void  BFSTraverse(GraphAdjList  GL)
{
	int  i;
	EdgeNode  *p;
	Queue  Q;

	for  (i  =  0;  i  <  GL->numVertexes;  i++)
	{
		visited[i]  =  FALSE;
	}

	InitQueue(&Q);

	for  (i  =  0;  i  <  GL->numVertexes;  i++)
	{
		if  (!visited[i])
		{
			visited[i]  =  TRUE;

			/*  打印顶点，也可以其他操作  */
			printf("%c  ",  GL->adjList[i].data);        
			EnQueue(&Q,  i);
			while  (!QueueEmpty(Q))
			{
				DeQueue(&Q,  &i);	
				/*  找到当前顶点边表链表头指针  */
				p  =  GL->adjList[i].firstedge;           
				 while  (p)
				{
					/*  若此顶点未被访问  */
					if  (!visited[p->adjvex])              
					{
						visited[p->adjvex]  =  TRUE;
						printf("%c  ",  GL->adjList[p->adjvex].data);
						/*  将此顶点入队列  */EnQueue(&Q,  p->adjvex);       
					 }
					/*  指针指向下一个邻接点  */
					p  =  p->next;                                      
				}
			}
		}
	}
}

对比图的深度优先遍历与广度优先遍历算法，你会发现，它们在时间复杂度上是一样的，不同之处仅仅在于对顶点访问的顺序不同。
可见两者在全图遍历上是没有优劣之分的，只是视不同的情况选择不同的算法。
不过如果图顶点和边非常多，不能在短时间内遍历完成，遍历的目的是为了寻找合适的顶点，那么选择哪种遍历就要仔细斟酌了。
深度优先更适合目标比较明确，以找到目标为主要目的的情况，而广度优先更适合在不断扩大遍历范围时找到相对最优解的情况。

最小生成树

我们把构造连通网的最小代价生成树称为最小生成树（Minimum Cost SpanningTree）。

普里姆（Prim）算法


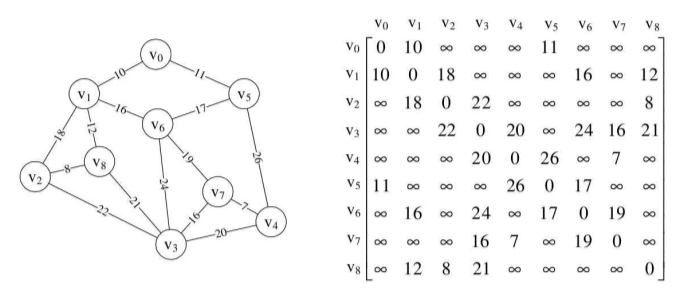
普里姆（Prim）算法代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
/*  Prim算法生成最小生成树  */
void  MiniSpanTree_Prim(MGraph  G)
{
	int  min,  i,  j,  k;
	/*  保存相关顶点下标  */
	int  adjvex[MAXVEX];                                                
	/*  保存相关顶点间边的权值  */
	int  lowcost[MAXVEX];                                              
	/*  初始化第一个权值为0，即v0加入生成树  */
	/*  lowcost的值为0，在这里就是此下标的顶点已经加入生成树  */
	lowcost[0]  =  0;                                                        
	/*  初始化第一个顶点下标为0  */
	adjvex[0]  =  0;
                                                          
	/*  循环除下标为0外的全部顶点  */
	for  (i  =  1;  i  <  G.numVertexes;  i++)            
	{
		/*  将v0顶点与之有边的权值存入数组  */
		lowcost[i]  =  G.arc[0][i];                            
		/*  初始化都为v0的下标  */
		adjvex[i]  =  0;                                       
	}

	for  (i  =  1;  i  <  G.numVertexes;  i++)
	{
		/*  初始化最小权值为∞，  */
		/*  通常设置为不可能的大数字如32767、65535等  */
		min  =  INFINITY;                                      
		j  =  1;  k  =  0;

		/*  循环全部顶点  */
		while  (j  <  G.numVertexes)                           
		{
			/*  如果权值不为0且权值小于min  */
			if  (lowcost[j]  !=  0  &&  lowcost[j]  <  min)
			{                                                      
				/*  则让当前权值成为最小值  */
				min  =  lowcost[j];                            
				/*  将当前最小值的下标存入k  */
				k  =  j;                                               
			}
			j++;
		}

		/*  打印当前顶点边中权值最小边  */
		printf("(%d,%d)",  adjvex[k],  k);              
		/*  将当前顶点的权值设置为0，表示此顶点已经完成任务  */
		lowcost[k]  =  0; 
                                     
		/*  循环所有顶点  */
		for  (j  =  1;  j  <  G.numVertexes;  j++)        
		{
			/*  若下标为k顶点各边权值小于此前这些顶点未被加入生成树权值  */
			if  (lowcost[j]  !=  0  &&  G.arc[k][j]  <  lowcost[j])
			{                                                      
				/*  将较小权值存入lowcost  */
				lowcost[j]  =  G.arc[k][j];            
				/*  将下标为k的顶点存入adjvex  */
				adjvex[j]  =  k;                                  
			}
		}
	}
}

1．
程序开始运行，我们由第4～5行，创建了两个一维数组lowcost和adjvex，长度都为顶点个数9。

2．
第6～7行我们分别给这两个数组的第一个下标位赋值为0，adjvex[0]=0其实意思就是我们现在从顶点v0开始（事实上，最小生成树从哪个顶点开始计算都无所谓，我们假定从v0开始），lowcost[0]=0就表示v0已经被纳入到最小生成树中，之后凡是lowcost数组中的值被设置为0就是表示此下标的顶点被纳入最小生成树。

3．
第8～12行表示我们读取邻接矩阵的第一行数据。
将数值赋值给lowcost数组，所以此时lowcost数组值为{0,10,65535,65535,65535,11,65535,65535,65535}，而adjvex则全部为0。
此时，我们已经完成了整个初始化的工作，准备开始生成。

4．
第13～36行，整个循环过程就是构造最小生成树的过程。

5．
第15～16行，将min设置为了一个极大值65535，它的目的是为了之后找到一定范围内的最小权值。
j是用来做顶点下标循环的变量，k是用来存储最小权值的顶点下标。

6．
第17～25行，循环中不断修改min为当前lowcost数组中最小值，并用k保留此最小值的顶点下标。经过循环后，min=10，k=1。
注意19行if判断的lowcost[j]!=0表示已经是生成树的顶点不参与最小权值的查找。

7．
第26行，因k=1，adjvex[1]=0，所以打印结果为(0,1)，表示v0至v1边为最小生成树的第一条边。如图所示。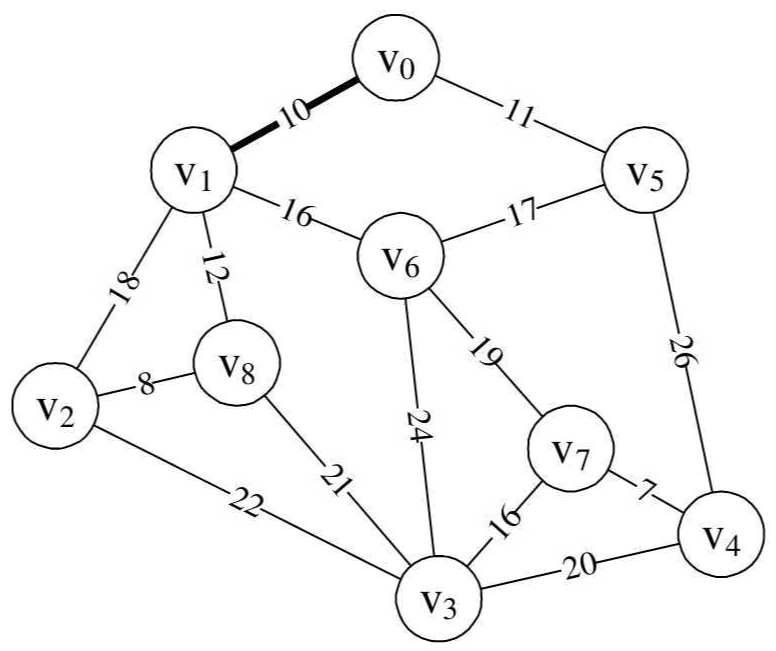

8．
第27行，此时因k=1我们将lowcost[k]=0就是说顶点v1纳入到最小生成树中。
此时lowcost数组值为{0,0,65535,65535,65535,11,65535,65535,65535}。

9．
第28～35行，j循环由1至8，因k=1，查找邻接矩阵的第v1行的各个权值，与low-cost的对应值比较，若更小则修改low-cost值，并将k值存入adjvex数组中。
因第v1行有18、16、12均比65535小，所以最终lowcost数组的值为：{0,0,18,65535,65535,11,16,65535,12}。adjvex数组的值为：{0,0,1,0,0,0,1,0,1}。
这里第30行if判断的lowcost[j]!=0也说明v0和v1已经是生成树的顶点不参与最小权值的比对了。

10．再次循环，由第15行到第26行，此时min=11，k=5，adjvex[5]=0。因此打印结构为(0,5)。
表示v0至v5边为最小生成树的第二条边，如图所示。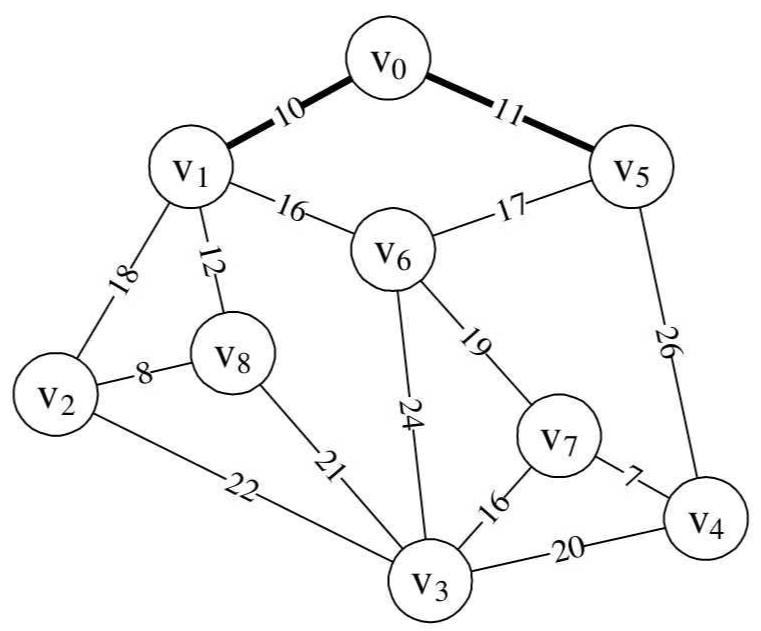

11．接下来执行到36行，lowcost数组的值为：{0,0,18,65535,26,0,16,65535,12}。ad-jvex数组的值为：{0,0,1,0,5,0,1,0,1}。

12．之后，相信大家也都会自己去模拟了。通过不断的转换，构造的过程如图中图1～图6所示。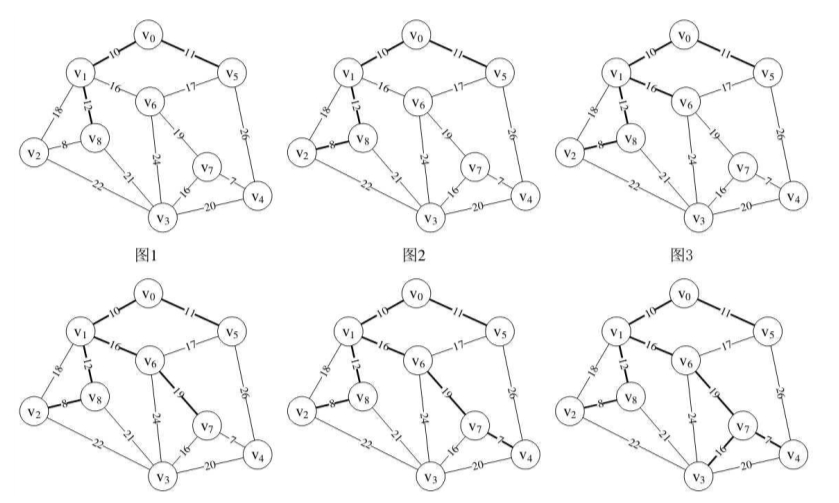

有了这样的讲解，再来介绍普里姆（Prim）算法的实现定义可能就容易理解一些。

假设N=(V,{E})是连通网，TE是N上最小生成树中边的集合。算法从U={u0}(u0∈V)，TE={}开始。重复执行下述操作：在所有u∈U,v∈V-U的边(u,v)∈E中找一条代价最小的边(u0,v0)并入集合TE，同时v0并入U，直至U=V为止。此时TE中必有n-1条边，则T=(V,{TE})为N的最小生成树。

由算法代码中的循环嵌套可得知此算法的时间复杂度为O(n2)。

克鲁斯卡尔（Kruskal）算法

现在我们来换一种思考方式，普里姆（Prim）算法是以某顶点为起点，逐步找各顶点上最小权值的边来构建最小生成树的。

同样的思路，我们也可以直接就以边为目标去构建，因为权值是在边上，直接去找最小权值的边来构建生成树也是很自然的想法，只不过构建时要考虑是否会形成环路而已。
此时我们就用到了图的存储结构中的边集数组结构。

以下是edge边集数组结构的定义代码：

1
2
3
4
5
6
7
/*  对边集数组Edge结构的定义  */
typedef  struct
{
	int  begin;
	int  end;
	int  weight;
}  Edge;

我们将之前的邻接矩阵通过程序转化为下图右图的边集数组，并且对它们按权值从小到大排序。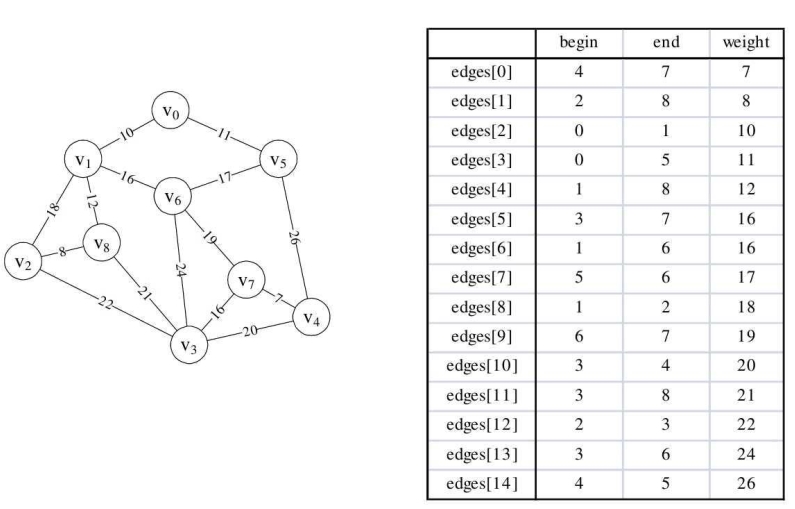

于是克鲁斯卡尔（Kruskal）算法代码如下，左侧数字为行号。
其中MAXEDGE为边数量的极大值，此处大于等于15即可，MAXVEX为顶点个数最大值，此处大于等于9即可。
现在假设我们自己就是计算机，在调用MiniSpanTree_Kruskal函数，输入上图右图的邻接矩阵后，看看它是如何运行并打印出最小生成树的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/*  Kruskal算法生成最小生成树  */

/*  生成最小生成树  */
void  MiniSpanTree_Kruskal(MGraph  G)          
{
	int  i,  n,  m;
	/*  定义边集数组  */
	Edge  edges[MAXEDGE];                                
	/*  定义一数组用来判断边与边是否形成环路  */
	int  parent[MAXVEX];                                  
	/*  此处省略将邻接矩阵G转化为边集数组edges并按权由小到大排序的代码  */

	for  (i  =  0;  i  <  G.numVertexes;  i++)
	{
		/*  初始化数组值为0  */
		parent[i]  =  0;     
	}
                               
	/*  循环每一条边  */
	for  (i  =  0;  i  <  G.numEdges;  i++)        
	{
		n  =  Find(parent,  edges[i].begin);
		m  =  Find(parent,  edges[i].end);
		/*  假如n与m不等，说明此边没有与现有生成树形成环路  */
		if  (n  !=  m)                                          
		{
			/*  将此边的结尾顶点放入下标为起点的parent中  */
			/*  表示此顶点已经在生成树集合中  */
			parent[n]  =  m;                            
			printf("(%d,  %d)  %d  ",  edges[i].begin,  edges[i].end,  edges[i].weight);
		}
	}
}

/*  查找连线顶点的尾部下标  */
int  Find(int  *parent,  int  f)                        
{
	while  (parent[f]  >  0)
	{
		f  =  parent[f];
	}

	return  f;
}

1．
程序开始运行，第5行之后，我们省略掉颇占篇幅但却很容易实现的将邻接矩阵转换为边集数组，并按权值从小到大排序的代码，也就是说，在第5行开始，我们已经有了结构为edge，数据内容是前图的右图的一维数组edges。

2．
第5～7行，我们声明一个数组parent，并将它的值都初始化为0，它的作用我们后面慢慢说。

3．
第8～17行，我们开始对边集数组做循环遍历，开始时，i=0。

4．
第10行，我们调用了第19～25行的函数Find，传入的参数是数组parent和当前权值最小边(v4,v7)的begin:4。
因为parent中全都是0所以传出值使得n=4。

5．
第11行，同样作法，传入(v4,v7)的end:7。
传出值使得m=7。

6．
第12～16行，很显然n与m不相等，因此parent[4]=7。
此时parent数组值为{0,0,0,0,7,0,0,0,0}，并且打印得到“(4,7)7”。
此时我们已经将边(v4,v7)纳入到最小生成树中，如图所示。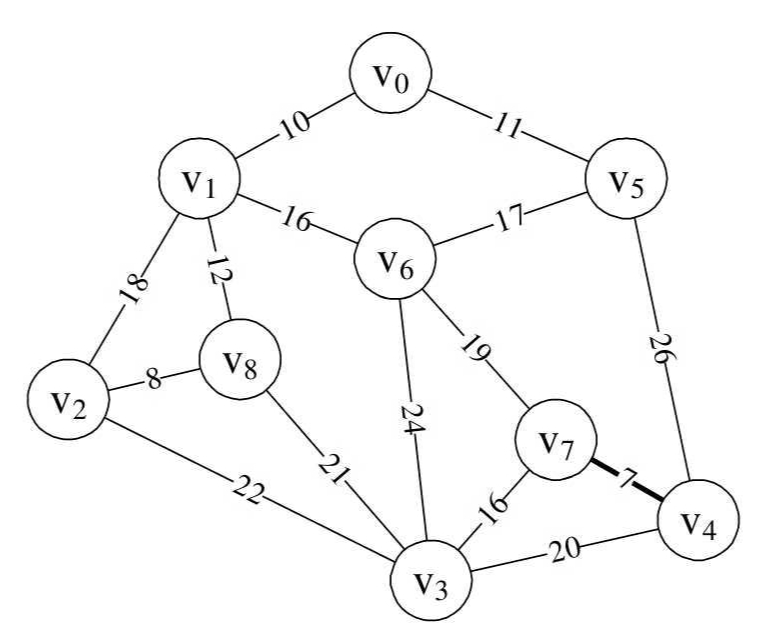

7．
循环返回，执行10～16行，此时i=1，edge[1]得到边(v2,v8)，n=2，m=8，parent[2]=8，打印结果为“(2,8)8”，此时parent数组值为{0,0,8,0,7,0,0,0,0}，这也就表示边(v4,v7)和边(v2,v8)已经纳入到最小生成树，如图所示。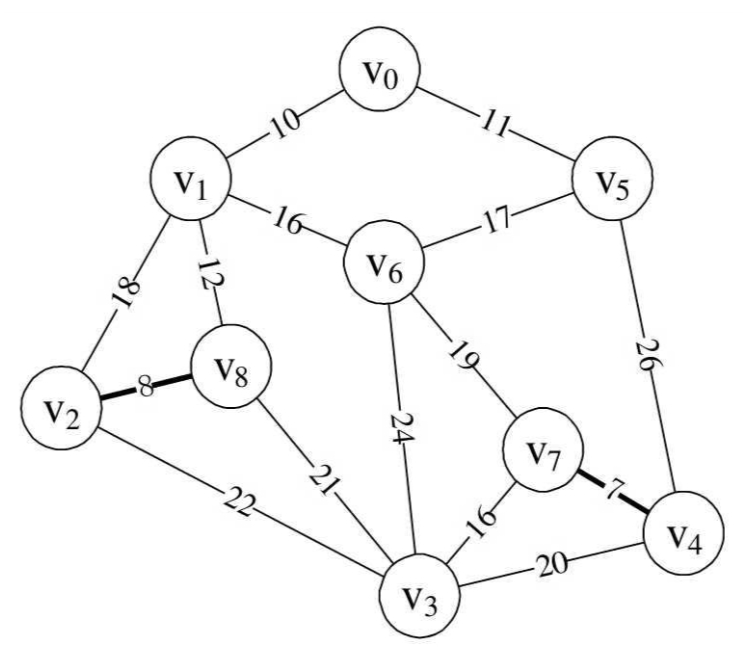

8．
再次执行10～16行，此时i=2，edge[2]得到边(v0,v1)，n=0，m=1，parent[0]=1，打印结果为“(0,1)10”，此时parent数组值为{1,0,8,0,7,0,0,0,0}，此时边(v4,v7)、(v2,v8)和(v0,v1)已经纳入到最小生成树，如图所示。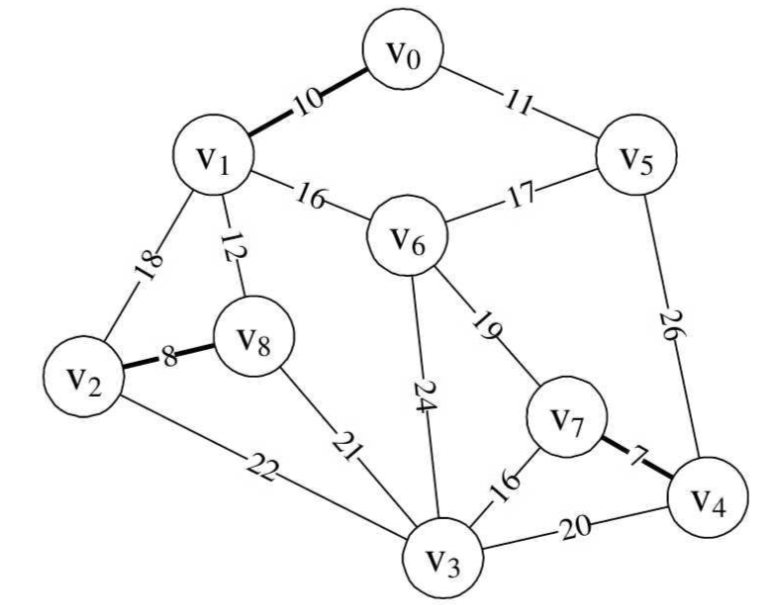

9．
当i=3、4、5、6时，分别将边(v0,v5)、(v1,v8)、(v3,v7)、(v1,v6)纳入到最小生成树中，如图所示。
此时parent数组值为{1,5,8,7,7,8,0,0,6}，怎么去解读这个数组现在这些数字的意义呢？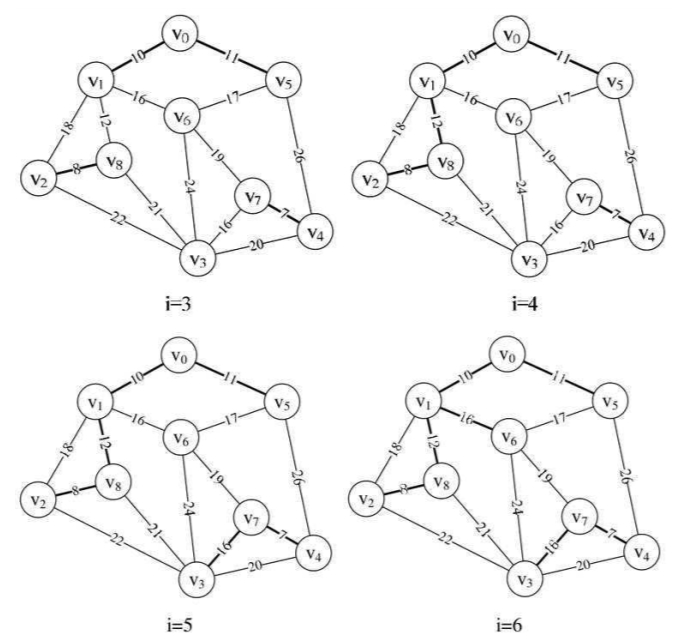

从上图的右下方的图i=6的粗线连线可以得到，我们其实是有两个连通的边集合A与B中纳入到最小生成树中的，如下图所示。
当parent[0]=1，表示v0和v1已经在生成树的边集合A中。
此时将parent[0]=1的1改为下标，由parent[1]=5，表示v1和v5在边集合A中，parent[5]=8表示v5与v8在边集合A中，parent[8]=6表示v8与v6在边集合A中，parent[6]=0表示集合A暂时到头，此时边集合A有v0、v1、v5、v8、v6。
我们查看parent中没有查看的值，parent[2]=8表示v2与v8在一个集合中，因此v2也在边集合A中。
再由parent[3]=7、parent[4]=7和parent[7]=0可知v3、v4、v7在另一个边集合B中。

10．
当i=7时，第10行，调用Find函数，会传入参数edges[7].begin=5。
此时第21行，parent[5]=8>0，所以f=8，再循环得parent[8]=6。
因parent[6]=0所以Find返回后第10行得到n=6。
而此时第11行，传入参数edges[7].end=6得到m=6。此时n=m，不再打印，继续下一循环。
这就告诉我们，因为边(v5,v6)使得边集合A形成了环路。因此不能将它纳入到最小生成树中，如上图所示。

11．
当i=8时，与上面相同，由于边(v1,v2)使得边集合A形成了环路。
因此不能将它纳入到最小生成树中，如上图所示。

12．
当i=9时，边(v6,v7)，第10行得到n=6，第11行得到m=7，因此parent[6]=7，打印“(6,7)19”。此时parent数组值为{1,5,8,7,7,8,7,0,6}，如图所示。

13．
此后边的循环均造成环路，最终最小生成树即为图所示。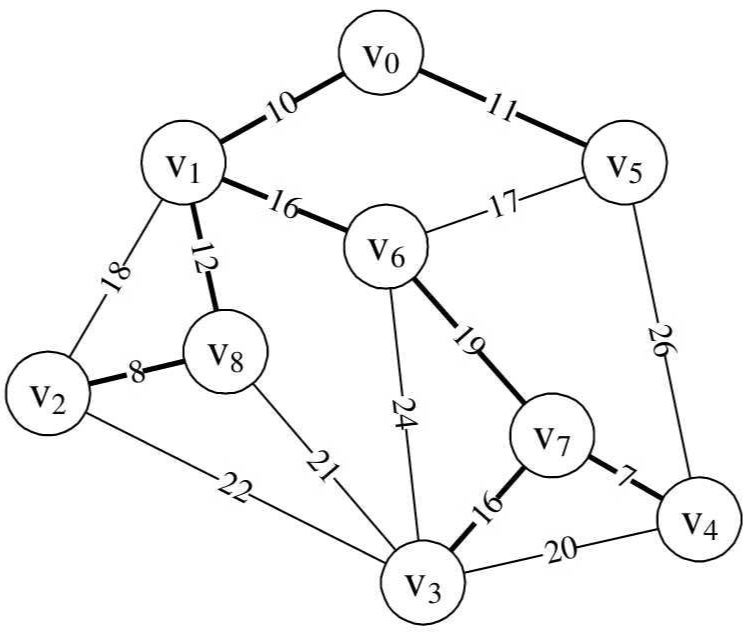

好了，我们来把克鲁斯卡尔（Kruskal）算法的实现定义归纳一下结束这一节的讲解。

假设N=(V,{E})是连通网，则令最小生成树的初始状态为只有n个顶点而无边的非连通图T={V,{}}，图中每个顶点自成一个连通分量。在E中选择代价最小的边，若该边依附的顶点落在T中不同的连通分量上，则将此边加入到T中，否则舍去此边而选择下一条代价最小的边。依次类推，直至T中所有顶点都在同一连通分量上为止。

此算法的Find函数由边数e决定，时间复杂度为O(loge)，而外面有一个for循环e次。所以克鲁斯卡尔算法的时间复杂度为O(eloge)。

对比两个算法，克鲁斯卡尔算法主要是针对边来展开，边数少时效率会非常高，所以对于稀疏图有很大的优势；而普里姆算法对于稠密图，即边数非常多的情况会更好一些。

最短路径

在网图和非网图中，最短路径的含义是不同的。
由于非网图它没有边上的权值，所谓的最短路径，其实就是指两顶点之间经过的边数最少的路径；而对于网图来说，最短路径，是指两顶点之间经过的边上权值之和最少的路径，并且我们称路径上的第一个顶点是源点，最后一个顶点是终点。
显然，我们研究网图更有实际意义，就地图来说，距离就是两顶点间的权值之和。
而非网图完全可以理解为所有的边的权值都为1的网。

迪杰斯特拉（Dijkstra）算法

这是一个按路径长度递增的次序产生最短路径的算法。它的思路大体是这样的。

比如说要求下图中顶点v0到顶点v1的最短距离，没有比这更简单的了，答案就是1，路径就是直接v0连线到v1。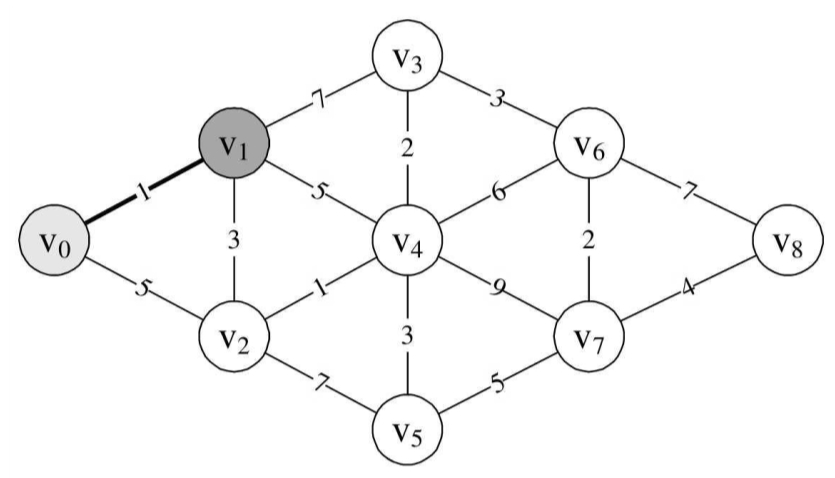

由于顶点v1还与v2、v3、v4连线，所以此时我们同时求得了v0→v1→v2=1+3=4，v0→v1→ v3=1+7=8，v0→v1→v4=1+5=6。
现在，我问v0到v2的最短距离，如果你不假思索地说是5，那就犯错了。
因为边上都有权值，刚才已经有v0→v1→v2的结果是4，比5还要小1个单位，它才是最短距离，如图所示。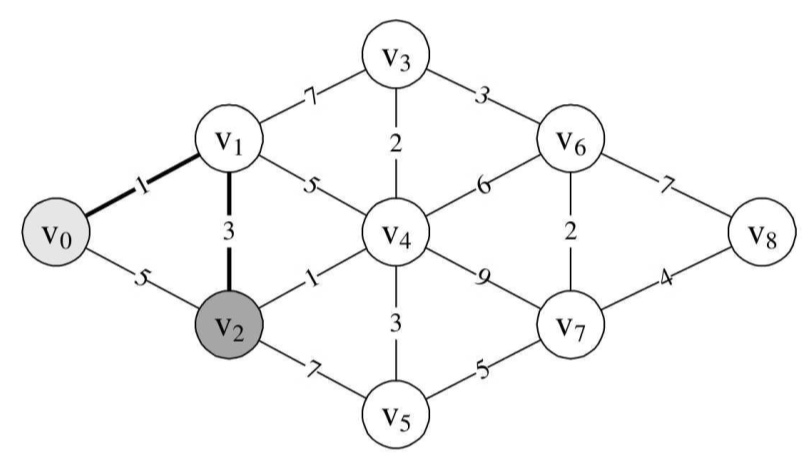

由于顶点v2还与v4、v5连线，所以此时我们同时求得了v0→v2→v4其实就是v0→v1→v2→v4=4+1=5，v0→v2→v5=4+7=11。
这里v0→v2我们用的是刚才计算出来的较小的4。
此时我们也发现v0→v1→v2→v4=5要比v0→v1→v4=6还要小。
所以v0到v4目前的最小距离是5，如图所示。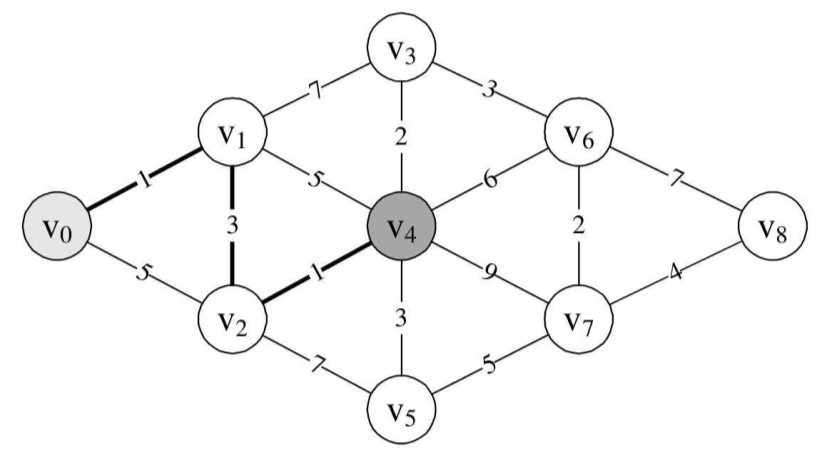

当我们要求v0到v3的最短距离时，通向v3的三条边，除了v6没有研究过外，v0→v1→v3的结果是8，而v0→v4→v3=5+2=7。
因此，v0到v3的最短距离是7，如图所示。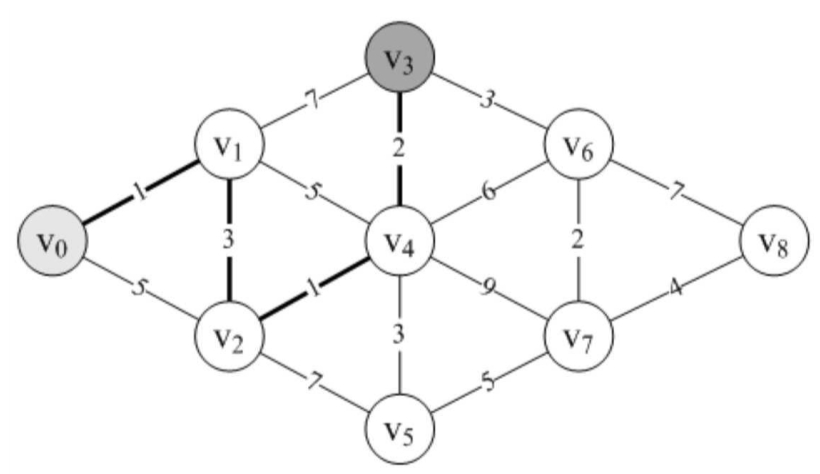

好了，我想你大致明白，这个迪杰斯特拉（Di-jkstra）算法是如何干活的了。
它并不是一下子就求出了v0到v8的最短路径，而是一步步求出它们之间顶点的最短路径，过程中都是基于已经求出的最短路径的基础上，求得更远顶点的最短路径，最终得到你要的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#define  MAXVEX  9
#define  INFINITY  65535
typedef  int  
/*  用于存储最短路径下标的数组  */
Patharc[MAXVEX];                                              
typedef  int  
/*  用于存储到各点最短路径的权值和  */
ShortPathTable[MAXVEX];
                                
/*  Dijkstra算法，求有向网G的v0顶点到其余顶点v最短路径P[v]及带权长度D[v]  */
/*  P[v]的值为前驱顶点下标，D[v]表示v0到v的最短路径长度和。  */
void  ShortestPath_Dijkstra(MGraph  G,  int  v0,  Patharc  *P,  ShortPathTable  *D)
{
	int  v,  w,  k,  min;
	/*  final[w]=1表示求得顶点v0至vw的最短路径  */
	int  final[MAXVEX];                                                    
	/*  初始化数据  */
	for  (v  =  0;  v  <  G.numVertexes;  v++)                  
	{
		/*  全部顶点初始化为未知最短路径状态  */
		final[v]  =  0;                                                      
		/*  将与v0点有连线的顶点加上权值  */
		(*D)[v]  =  G.arc[v0][v];                                  
		/*  初始化路径数组P为-1  */
		(*P)[v]  =  -1;                                                      
	}
	/*  v0至v0路径为0  */
	(*D)[v0]  =  0;
   	/*  v0至v0不需要求路径  */
	final[v0]  =  1;
                                                            
	/*  开始主循环，每次求得v0到某个v顶点的最短路径  */
	for  (v  =  1;  v  <  G.numVertexes;  v++)
	{
		/*  当前所知离v0顶点的最近距离  */
		min=INFINITY;                                                      
		/*  寻找离v0最近的顶点  */
		for  (w  =  0;  w  <  G.numVertexes;  w++)          
		{
			if  (!final[w]  &&  (*D)[w]  <  min)
			{
				k=w;
				/*  w顶点离v0顶点更近  */
				min  =  (*D)[w];                                    
			}
		}
		/*  将目前找到的最近的顶点置为1  */
		final[k]  =  1;                                                      
		/*  修正当前最短路径及距离  */
		for  (w  =  0;  w  <  G.numVertexes;  w++)          
		{      
			/*  如果经过v顶点的路径比现在这条路径的长度短的话  */
			if  (!final[w]  &&  (min  +  G.arc[k][w]  <  (*D)[w]))
			{                                                                      
				/*  说明找到了更短的路径，修改D[w]和P[w]  */
				/*  修改当前路径长度  */
				(*D)[w]  =  min  +  G.arc[k][w];        
				(*P)[w]=k;
			}
		}
	}
}

调用此函数前，我们需要为下图的左图准备邻接矩阵MGraph的G，如下图的右图，并且定义参数v0为0。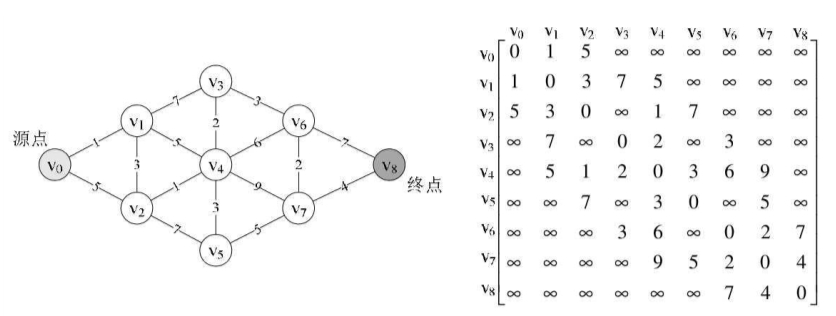

1．
程序开始运行，第4行final数组是为了v0到某顶点是否已经求得最短路径的标记，如果v0到vw已经有结果，则final[w]=1。

2．
第5～10行，是在对数据进行初始化的工作。
此时final数组值均为0，表示所有的点都未求得最短路径。
D数组为{65535,1,5,65535,65535,65535,65535,65535,65535}。
因为v0与v1和v2的边权值为1和5。
P数组全为0，表示目前没有路径。

3．
第11行，表示v0到v0自身，权值和结果为0。
D数组为{0,1,5,65535,65535,65535,65535,65535,65535}。
第12行，表示v0点算是已经求得最短路径，因此final[0]=1。
此时final数组为{1,0,0,0,0,0,0,0,0}。此时整个初始化工作完成。

4．
第13～33行，为主循环，每次循环求得v0与一个顶点的最短路径。因此v从1而不是0开始。

5．
第15～23行，先令min为65535的极大值，通过w循环，与D[w]比较找到最小值min=1，k=1。

6．
第24行，由k=1，表示与v0最近的顶点是v1，并且由D[1]=1，知道此时v0到v1的最短距离是1。因此将v1对应的final[1]设置为1。此时final数组为{1,1,0,0,0,0,0,0,0}。

7．
第25～32行是一循环，此循环甚为关键。
它的目的是在刚才已经找到v0与v1的最短路径的基础上，对v1与其他顶点的边进行计算，得到v0与它们的当前最短距离，如图所示。
因为min=1，所以本来D[2]=5，现在v0→v1→v2=D[2]=min+3=4，v0→v1→v3=D[3]=min+7=8，v0→v1→v4=D[4]=min+5=6，因此，D数组当前值为{0,1,4,8,6,65535,65535,65535,65535}。
而P[2]=1，P[3]=1，P[4]=1，它表示的意思是v0到v2、v3、v4点的最短路径它们的前驱均是v1。
此时P数组值为：{0,0,1,1,1,0,0,0,0}。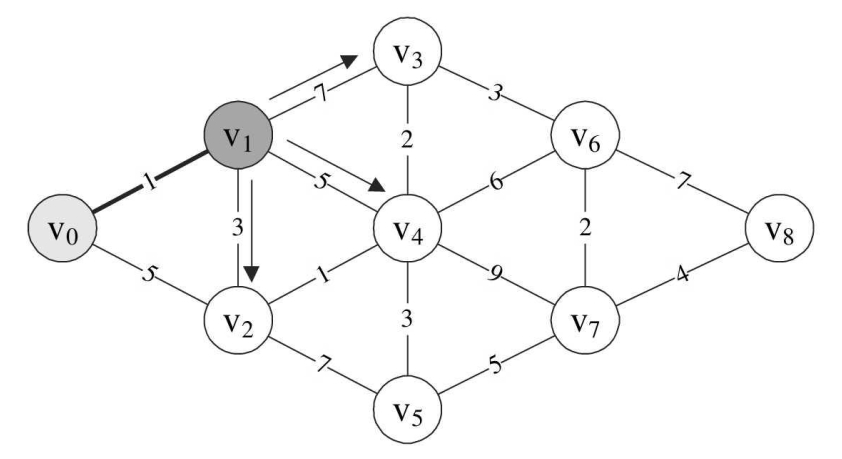

8．
重新开始循环，此时v=2。
第15～23行，对w循环，注意因为final[0]=1和final[1]=1，由第18行的!final[w]可知，v0与v1并不参与最小值的获取。通过循环比较，找到最小值min=4，k=2。

9．
第24行，由k=2，表示已经求出v0到v2的最短路径，并且由D[2]=4，知道最短距离是4。
因此将v2对应的final[2]设置为1，此时final数组为：{1,1,1,0,0,0,0,0,0}。

10．
第25～32行。在刚才已经找到v0与v2的最短路径的基础上，对v2与其他顶点的边，进行计算，得到v0与它们的当前最短距离，如图所示。
因为min=4，所以本来D[4]=6，现在v0→v2→v4=D[4]=min+1=5，v0→v2→v5=D[5]=min+7=11，因此，D数组当前值为：{0,1,4,8,5,11,65535,65535,65535}。
而原本P[4]=1，此时P[4]=2，P[5]=2，它表示v0到v4、v5点的最短路径它们的前驱均是v2。此时P数组值为：{0,0,1,1,2,2,0,0,0}。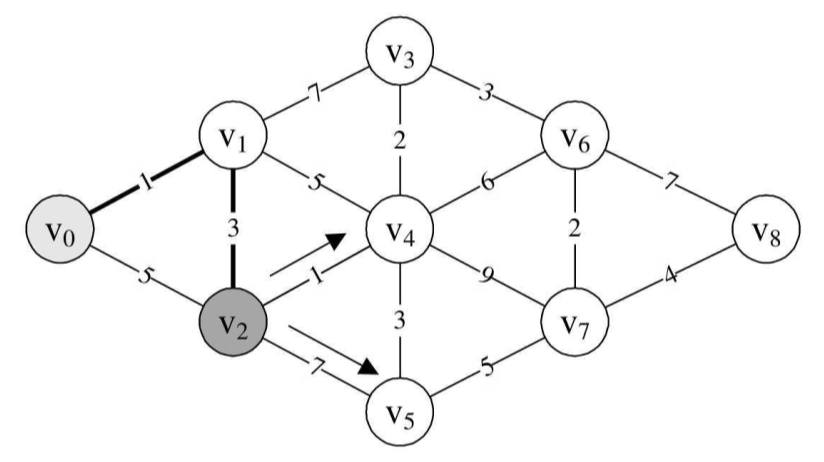

11．
重新开始循环，此时v=3。
第15～23行，通过对w循环比较找到最小值min=5，k=4。

12．
第24行，由k=4，表示已经求出v0到v4的最短路径，并且由D[4]=5，知道最短距离是5。因此将v4对应的final[4]设置为1。
此时final数组为：{1,1,1,0,1,0,0,0,0}。

13．
第25～32行。对v4与其他顶点的边进行计算，得到v0与它们的当前最短距离，如图所示。
因为min=5，所以本来D[3]=8，现在v0→v4→v3=D[3]=min+2=7，本来D[5]=11，现在v0→v4→v5=D[5]=min+3=8，另外v0→v4→v6=D[6]=min+6=11，v0→v4→v7=D[7]=min+9=14，因此，D数组当前值为：{0,1,4,7,5,8,11,14,65535}。
而原本P[3]=1，此时P[3]=4，原本P[5]=2，此时P[5]=4，另外P[6]=4，P[7]=4，它表示v0到v3、v5、v6、v7点的最短路径它们的前驱均是v4。此时P数组值为：{0,0,1,4,2,4,4,4,0}。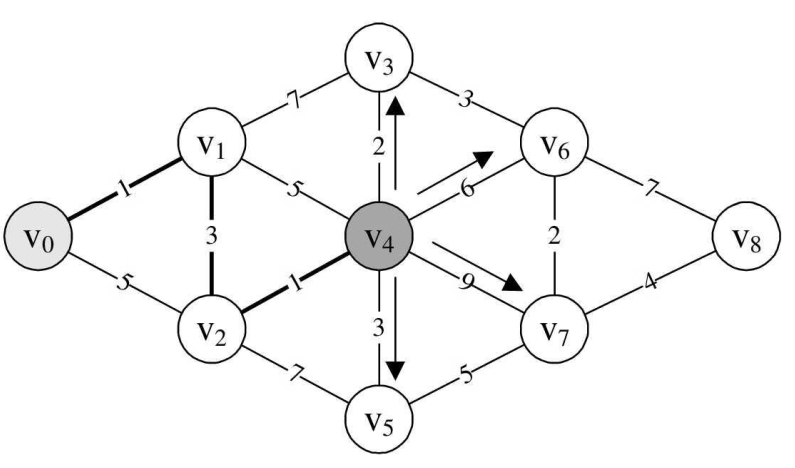

14．
之后的循环就完全类似了。得到最终的结果，如图所示。
此时final数组为：{1,1,1,1,1,1,1,1,1}，它表示所有的顶点均完成了最短路径的查找工作。
此时D数组为：{0,1,4,7,5,8,10,12,16}，它表示v0到各个顶点的最短路径数，比如D[8]=1+3+1+2+3+2+4=16。
此时的P数组为：{0,0,1,4,2,4,3,6,7}，这串数字可能略为难理解一些。比如P[8]=7，它的意思是v0到v8的最短路径，顶点v8的前驱顶点是v7，再由P[7]=6表示v7的前驱是v6，P[6]=3，表示v6的前驱是v3。这样就可以得到，v0到v8的最短路径为v8←v7←v6←v3←v4←v2←v1←v0，即v0→v1→v2→v4→v3→v6→v7→v8。

其实最终返回的数组D和数组P，是可以得到v0到任意一个顶点的最短路径和路径长度的。
例如v0到v8的最短路径并没有经过v5，但我们已经知道v0到v5的最短路径了。
由D[5]=8可知它的路径长度为8，由P[5]=4可知v5的前驱顶点是v4，所以v0到v5的最短路径是v0→v1→v2→v4→v5。

也就是说，我们通过迪杰斯特拉（Dijkstra）算法解决了从某个源点到其余各顶点的最短路径问题。
从循环嵌套可以很容易得到此算法的时间复杂度为O(n2)，尽管有同学觉得，可不可以只找到从源点到某一个特定终点的最短路径，其实这个问题和求源点到其他所有顶点的最短路径一样复杂，时间复杂度依然是O(n2)。

弗洛伊德（Floyd）算法

为了能讲明白弗洛伊德（Floyd）算法的精妙所在，我们先来看最简单的案例。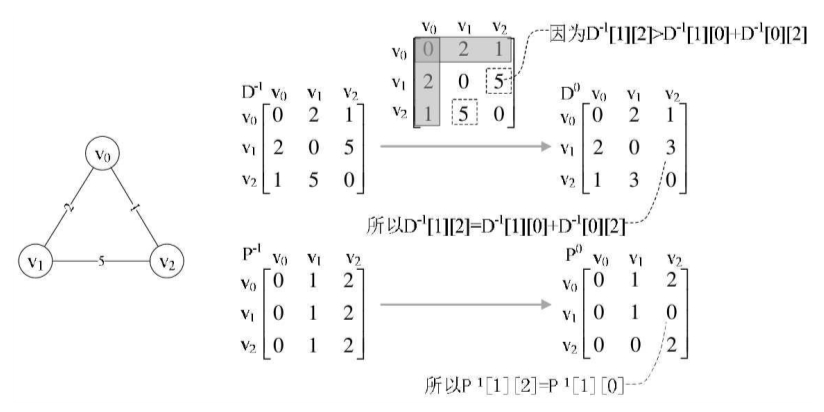

我们先定义两个二维数组D[3][3]和P[3][3]，D代表顶点到顶点的最短路径权值和的矩阵。P代表对应顶点的最小路径的前驱矩阵，用来存储路径。
在未分析任何顶点之前，我们将D命名为D-1，其实它就是初始的图的邻接矩阵。将P命名为P-1，初始化为图中所示的矩阵。

首先我们来分析，所有的顶点经过v0后到达另一顶点的最短路径。
因为只有三个顶点，因此需要查看v1→v0→v2，得到D-1[1][0]+D-1[0][2]=2+1=3。
D-1[1][2]表示的是v1→v2的权值为5，我们发现D-1[1][2]>D-1[1][0]+D-1[0][2]，通俗的话讲就是v1→v0→v2比直接v1→v2距离还要近。
所以我们就让D-1[1][2]=D-1[1][0]+D-1[0][2]=3，同样的D-1[2][1]=3，于是就有了D0的矩阵。
因为有变化，所以P矩阵对应的P-1[1][2]和P-1[2][1]也修改为当前中转的顶点v0的下标0，于是就有了P0。
也就是说D0[v][w]=min{D-1[v][w],D-1[v][0]+D-1[0][w]}

接下来，其实也就是在D0和P0的基础上继续处理所有顶点经过v1和v2后到达另一顶点的最短路径，得到D1和P1、D2和P2完成所有顶点到所有顶点的最短路径计算工作。

如果我就用这么简单的图形来讲解代码，大家一定会觉得不能说明什么问题。所以我们还是以前面的复杂网图为例，来讲解弗洛伊德（Floyd）算法。

首先我们针对下图的左网图准备两个矩阵D-1和P-1，D-1就是网图的邻接矩阵，P-1初设为P[i][j]=j这样的矩阵，它主要用来存储路径。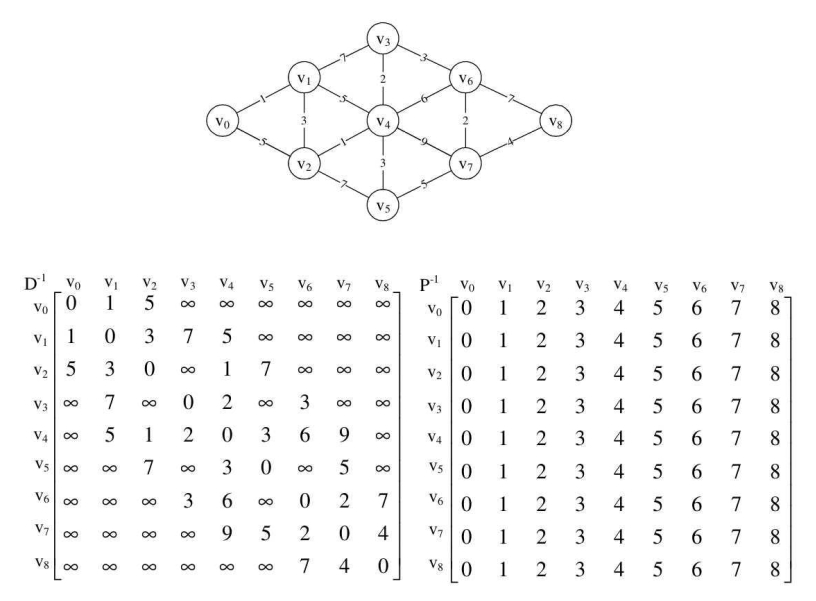

代码如下，注意因为是求所有顶点到所有顶点的最短路径，因此Pathmatirx和ShortPathTable都是二维数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
typedef  int  Pathmatirx[MAXVEX][MAXVEX];
typedef  int  ShortPathTable[MAXVEX][MAXVEX];

/*  Floyd算法，求网图G中各顶点v到其余顶点w最短路径P[v][w]及带权长度D[v][w]  */
void  ShortestPath_Floyd(MGraph  G,  Pathmatirx  *P,  ShortPathTable  *D)
{
	int  v,  w,  k;
	/*  初始化D与P  */
	for  (v  =  0;  v  <  G.numVertexes;  ++v)
	{
		for  (w  =  0;  w  <  G.numVertexes;  ++w)
		{
			/*  D[v][w]值即为对应点间的权值  */
			(*D)[v][w]  =  G.matirx[v][w];
			/*  初始化P  */
			(*P)[v][w]  =  w;
		}   
	}

    for  (k  =  0;  k  <  G.numVertexes;  ++k)
	{
		for  (v  =  0;  v  <  G.numVertexes;  ++v)
		{
			for  (w  =  0;  w  <  G.numVertexes;  ++w)
			{
				if  ((*D)[v][w]  >  (*D)[v][k]  +  (*D)[k][w])
				{                                                              
					/*  如果经过下标为k顶点路径比原两点间路径更短  */
					/*  将当前两点间权值设为更小的一个  */
					(*D)[v][w]  =  (*D)[v][k]  +  (*D)[k][w];
					/*  路径设置经过下标为k的顶点  */
					(*P)[v][w]  =  (*P)[v][k];
				}
			}
		}
	}
}

1．
程序开始运行，第4～11行就是初始化了D和P，使得它们成为上图的两个矩阵。
从矩阵也得到，v0→v1路径权值是1，v0→v2路径权值是5，v0→v3无边连线，所以路径权值为极大值65535。

2．
第12～25行，是算法的主循环，一共三层嵌套，k代表的就是中转顶点的下标。
v代表起始顶点，w代表结束顶点。

3．
当K=0时，也就是所有的顶点都经过v0中转，计算是否有最短路径的变化。
可惜结果是，没有任何变化，如图所示。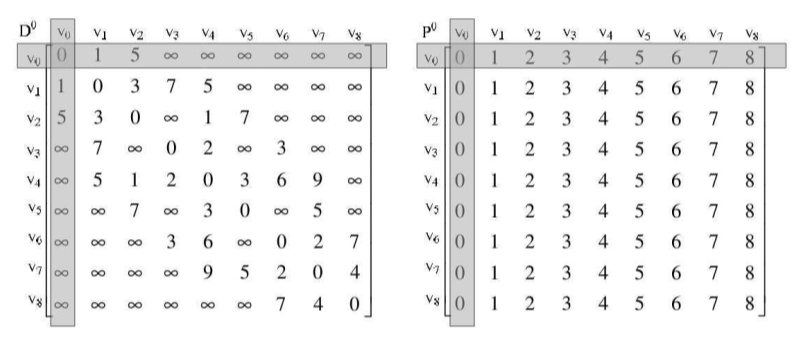

4．
当K=1时，也就是所有的顶点都经过v1中转。
此时，当v=0时，原本D[0][2]=5，现在由于D[0][1]+D[1][2]=4。
因此由代码的第20行，二者取其最小值，得到D[0][2]=4，同理可得D[0][3]=8、D[0][4]=6，当v=2、3、4时，也修改了一些数据，参考下图左图中虚线框数据。
由于这些最小权值的修正，所以在路径矩阵P上，也要作处理，将它们都改为当前的P[v][k]值，见代码第21行。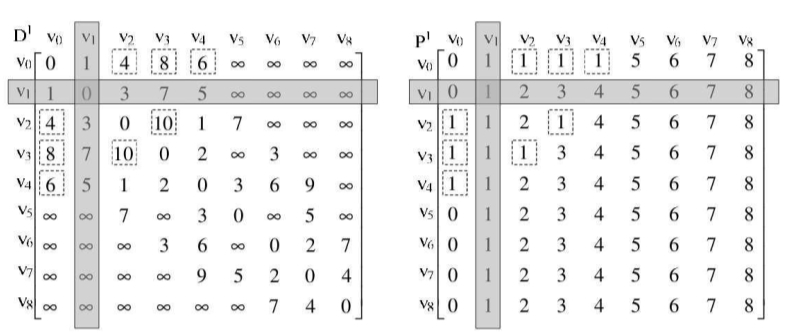

5.
接下来就是k=2一直到8结束，表示针对每个顶点做中转得到的计算结果，当然，我们也要清楚，D0是以D-1为基础，D1是以D0为基础，……，D8是以D7为基础，它们是有联系的，路径矩阵P也是如此。
最终当k=8时，两矩阵数据如图所示。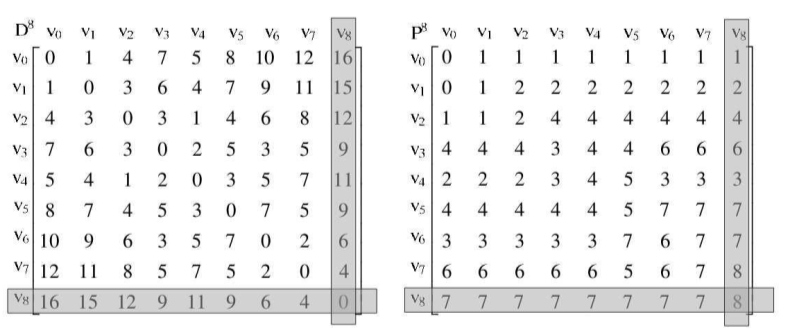

至此，我们的最短路径就算是完成了，你可以看到矩阵第v0行的数值与迪杰斯特拉（Dijkstra）算法求得的D数组的数值是完全相同，都是{0,1,4,7,5,8,10,12,16}。
而且这里是所有顶点到所有顶点的最短路径权值和都可以计算出。
那么如何由P这个路径数组得出具体的最短路径呢？以v0到v8为例，从上图的右图第v8列，P[0][8]=1，得到要经过顶点v1，然后将1取代0得到P[1][8]=2，说明要经过v2，然后将2取代1得到P[2][8]=4，说明要经过v4，然后将4取代2得到P[4][8]=3，说明要经过v3，……，这样很容易就推导出最终的最短路径值为v0→v1→v2→v4→v3→v6→v7→v8。
求最短路径的显示代码可以这样写。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
for  (v  =  0;  v  <  G.numVertexes;  ++v)
{
	for  (w  =  v  +  1;  w  <  G.numVertexes;  w++)
	{
		printf("v%d-v%d  weight:  %d  ",  v,  w,  D[v][w]);
		/*  获得第一个路径顶点下标  */
		k  =  P[v][w];                                
		/*  打印源点  */
		printf("  path:  %d",  v);          
		/*  如果路径顶点下标不是终点  */
		while  (k  !=  w)                            
		{
			/*  打印路径顶点  */printf("  ->  %d",  k);        
			/*  获得下一个路径顶点下标  */
			k  =  P[k][w];                        
		}
			/*  打印终点  */
			printf("  ->  %d\n",  w);            
	}
		printf("\n");
}

拓扑排序

拓扑排序介绍

在一个表示工程的有向图中，用顶点表示活动，用弧表示活动之间的优先关系，这样的有向图为顶点表示活动的网，我们称为AOV网（ActivityOn Vertex Network）。
AOV网中的弧表示活动之间存在的某种制约关系。
比如演职人员确定了，场地也联系好了，才可以开始进场拍摄。
另外就是AOV网中不能存在回路。
刚才已经举了例子，让某个活动的开始要以自己完成作为先决条件，显然是不可以的。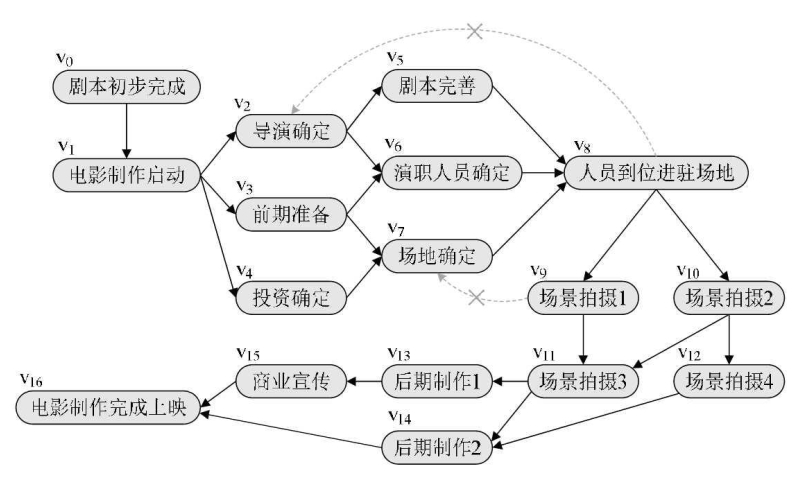

设G=(V,E)是一个具有n个顶点的有向图，V中的顶点序列v1，v2，……，vn，满足若从顶点vi到vj有一条路径，则在顶点序列中顶点vi必在顶点vj之前。则我们称这样的顶点序列为一个拓扑序列。

上图这样的AOV网的拓扑序列不止一条。序列v0v1v2v3v4v5v6v7v8v9v10v11v12v13v14v15v16是一条拓扑序列，而v0v1v4v3v2v7v6v5v8v10v9v12v11v14v13v15v16也是一条拓扑序列。

所谓拓扑排序，其实就是对一个有向图构造拓扑序列的过程。
构造时会有两个结果，如果此网的全部顶点都被输出，则说明它是不存在环（回路）的AOV网；如果输出顶点数少了，哪怕是少了一个，也说明这个网存在环（回路），不是AOV网。

一个不存在回路的AOV网，我们可以将它应用在各种各样的工程或项目的流程图中，满足各种应用场景的需要，所以实现拓扑排序的算法就很有价值了。

拓扑排序算法

对AOV网进行拓扑排序的基本思路是：从AOV网中选择一个入度为0的顶点输出，然后删去此顶点，并删除以此顶点为尾的弧，继续重复此步骤，直到输出全部顶点或者AOV网中不存在入度为0的顶点为止。

首先我们需要确定一下这个图需要使用的数据结构。
前面求最小生成树和最短路径时，我们用的都是邻接矩阵，但由于拓扑排序的过程中，需要删除顶点，显然用邻接表会更加方便。
因此我们需要为AOV网建立一个邻接表。
考虑到算法过程中始终要查找入度为0的顶点，我们在原来顶点表结点结构中，增加一个入度域in，结构如下所示，其中in就是入度的数字。

indata first edge

因此对于下图的第一幅图AOV网，我们可以得到如第二幅图的邻接表数据结构。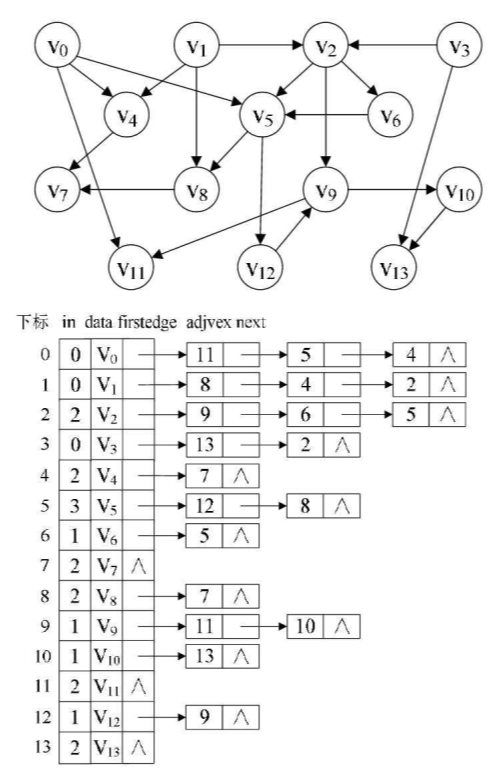

在拓扑排序算法中，涉及的结构代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/*  边表结点  */
typedef  struct  EdgeNode                    
{
	/*  邻接点域，存储该顶点对应的下标  */
	int  adjvex;                                    
	/*  用于存储权值，对于非网图可以不需要  */
	int  weight;                                    
	/*  链域，指向下一个邻接点  */
	struct  EdgeNode  *next;              
}  EdgeNode;

/*  顶点表结点  */
typedef  struct  VertexNode                
{
	/*  顶点入度*/
	int  in;                                            
	/*  顶点域，存储顶点信息  */
	int  data;                                        
	/*  边表头指针  */
	EdgeNode  *firstedge;                  
}  VertexNode,  AdjList[MAXVEX];

typedef  struct
{
	AdjList  adjList;
	/*  图中当前顶点数和边数  */
	int  numVertexes,numEdges;        
}  graphAdjList,  *GraphAdjList;

在算法中，我还需要辅助的数据结构—栈，用来存储处理过程中入度为0的顶点，目的是为了避免每个查找时都要去遍历顶点表找有没有入度为0的顶点。
现在我们来看代码，并且模拟运行它。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
/*  拓扑排序，若GL无回路，则输出拓扑排序序列并返回OK，若有回路返回ERROR  */
Status  TopologicalSort(GraphAdjList  GL)
{
	EdgeNode  *e;
	int  i,  k,  gettop;
	/*  用于栈指针下标  */
	int  top  =  0;      
	/*  用于统计输出顶点的个数  */
	int  count  =  0;                                                                                                   
	/*  建栈存储入度为0的顶点  */
	int  *stack;
   
    stack  =  (int  *)malloc(GL->numVertexes  *  sizeof(int));

	for  (i  =  0;  i  <  GL->numVertexes;  i++)
	{
		if  (GL->adjList[i].in  ==  0)
		{
			/*  将入度为0的顶点入栈  */
			stack[++top]  =  i;
		}
	}                                                    

	while  (top  !=  0)
	{
		/*  出栈  */
		gettop  =  stack[top--];                                                  
		/*  打印此顶点  */
		printf("%d  ->  ",  GL->adjList[gettop].data);        
		/*  统计输出顶点数  */
		count++;                                                                              
		
		/*  对此顶点弧表遍历  */
		for  (e  =  GL->adjList[gettop].firstedge;  e;  e  =  e->next)
		{                                                                                            
			k  =  e->adjvex;
			/*  将k号顶点邻接点的入度减1  */
			if  (!(--GL->adjList[k].in))                                
			{
				/*若为0则入栈，以便于下次循环输出  */
				stack[++top]  =  k;
			}                                            
		}
	}

	/*如果count小于顶点数，说明存在环  */
	if  (count  <  GL->numVertexes)                                              
	{
		return  ERROR;
	}
	else
	{
		return  OK;
	}
}

1．
程序开始运行，第3～7行都是变量的定义，其中stack是一个栈，用来存储整型的数字。

2．
第8～10行，作了一个循环判断，把入度为0的顶点下标都入栈，从下图可知，此时stack应该为：{0,1,3}，即v0、v1、v3的顶点入度为0，如图所示。

3．
第12～23行，while循环，当栈中有数据元素时，始终循环。

4．
第14～16行，v3出栈得到gettop=3。并打印此顶点，然后count加1。

5．
第17～22行，循环其实是对v3顶点对应的弧链表进行遍历，即下图中的灰色部分，找到v3连接的两个顶点v2和v13，并将它们的入度减少一位，此时v2和v13的in值都为1。
它的目的是为了将v3顶点上的弧删除。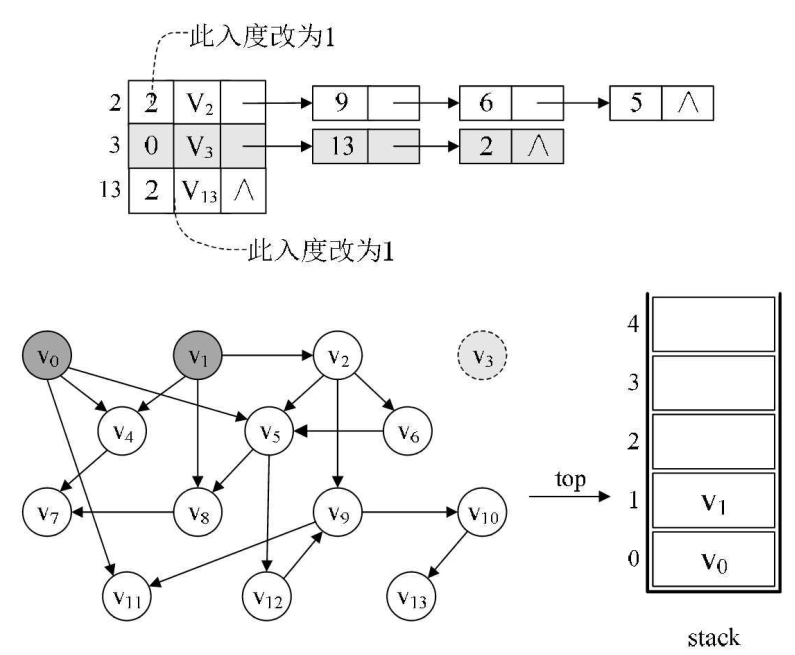

6．
再次循环，第12～23行。此时处理的是顶点v1。经过出栈、打印、count=2后，我们对v1到v2、v4、v8的弧进行了遍历。
并同样减少了它们的入度数，此时v2入度为0，于是由第20～21行知，v2入栈，如图所示。
试想，如果没有在顶点表中加入in这个入度数据域，20行的判断就必须要是循环，这显然是要消耗时间的，我们利用空间换取了时间。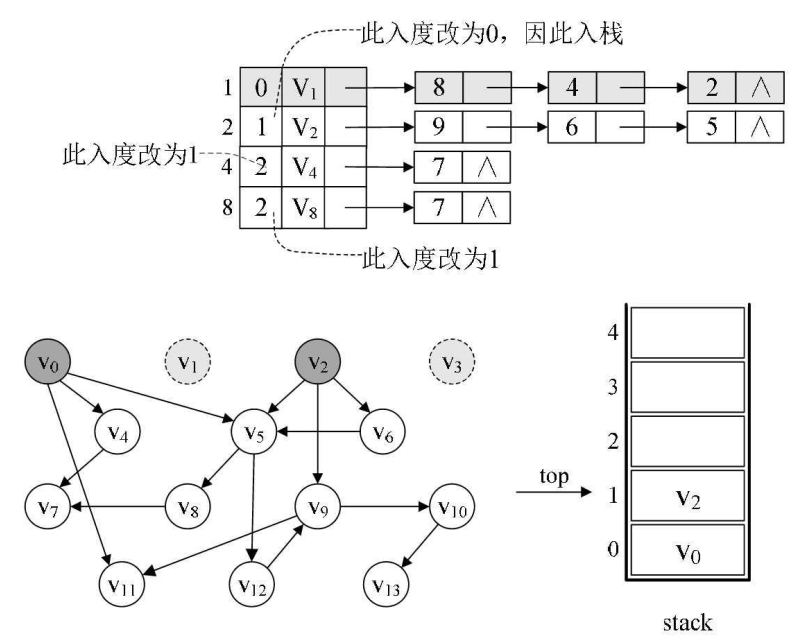

7．
接下来，就是同样的处理方式了。
下图展示了v2v6v0v4v5v8的打印删除过程，后面还剩几个顶点都类似，就不图示了。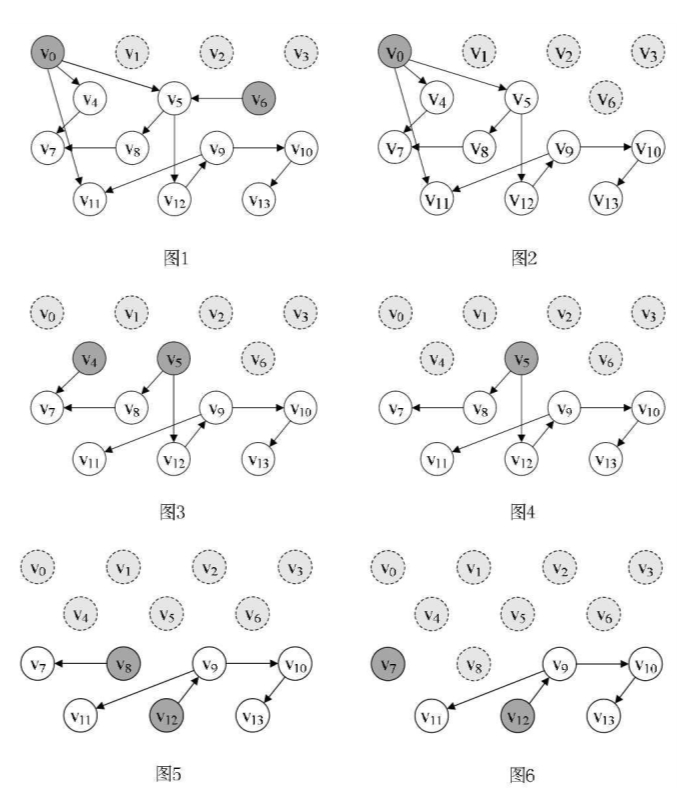

8．
最终拓扑排序打印结果为3->1->2->6->0->4->5->8->7->12->9->10->13->11。
当然这结果并不是唯一的一种拓扑排序方案。

分析整个算法，对一个具有n个顶点e条弧的AOV网来说，第8～10行扫描顶点表，将入度为0的顶点入栈的时间复杂为O(n)，而之后的while循环中，每个顶点进一次栈，出一次栈，入度减1的操作共执行了e次，所以整个算法的时间复杂度为O(n+e)。

关键路径

因此，我们如果要对一个流程图获得最短时间，就必须要分析它们的拓扑关系，并且找到当中最关键的流程，这个流程的时间就是最短时间。

因此在前面讲了AOV网的基础上，我们来介绍一个新的概念。
在一个表示工程的带权有向图中，用顶点表示事件，用有向边表示活动，用边上的权值表示活动的持续时间，这种有向图的边表示活动的网，我们称之为AOE网（Activity On Edge Net-work）。
我们把AOE网中没有入边的顶点称为始点或源点，没有出边的顶点称为终点或汇点。
由于一个工程，总有一个开始，一个结束，所以正常情况下，AOE网只有一个源点一个汇点。
例如下图就是一个AOE网。
其中v0即是源点，表示一个工程的开始，v9是汇点，表示整个工程的结束，顶点v0，v1，……，v9分别表示事件，弧<v0,v1>，<v0,v2>，……，<v8,v9>都表示一个活动，用a0，a1，……，a12表示，它们的值代表着活动持续的时间，比如弧<v0,v1>就是从源点开始的第一个活动a0，它的时间是3个单位。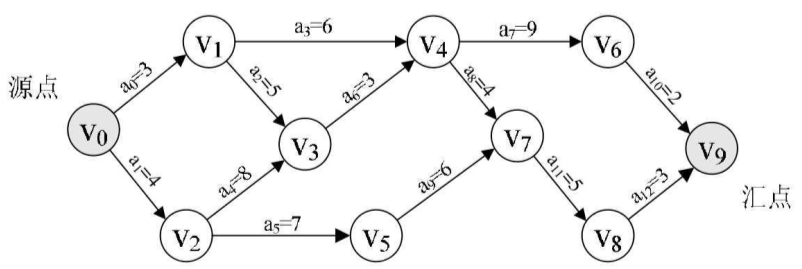

既然AOE网是表示工程流程的，所以它就具有明显的工程的特性。
如有在某顶点所代表的事件发生后，从该顶点出发的各活动才能开始。
只有在进入某顶点的各活动都已经结束，该顶点所代表的事件才能发生。

尽管AOE网与AOV网都是用来对工程建模的，但它们还是有很大的不同，主要体现在AOV网是顶点表示活动的网，它只描述活动之间的制约关系，而AOE网是用边表示活动的网，边上的权值表示活动持续的时间，如下图所示两图的对比。
因此，AOE网是要建立在活动之间制约关系没有矛盾的基础之上，再来分析完成整个工程至少需要多少时间，或者为缩短完成工程所需时间，应当加快哪些活动等问题。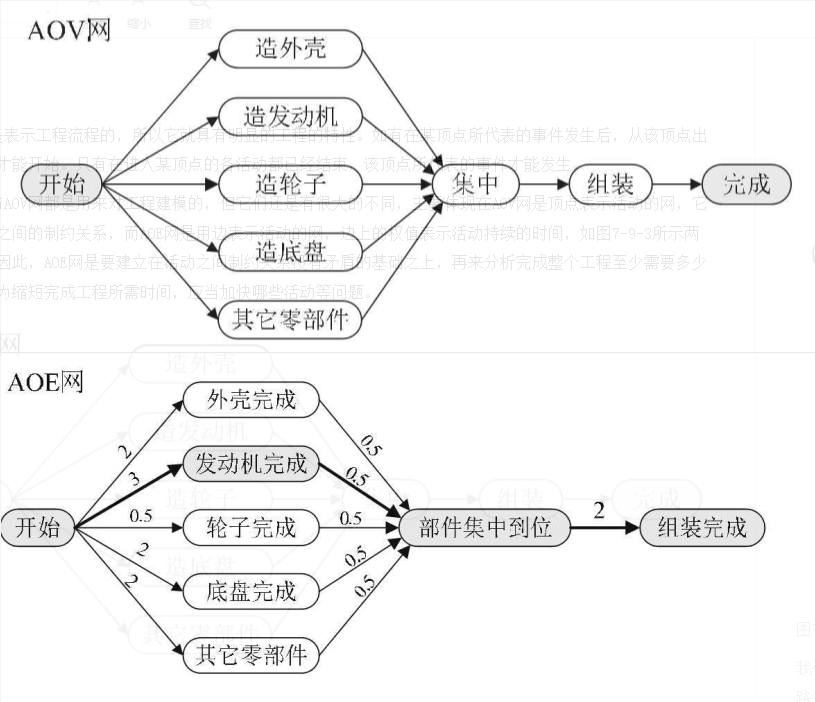

我们把路径上各个活动所持续的时间之和称为路径长度，从源点到汇点具有最大长度的路径叫关键路径，在关键路径上的活动叫关键活动。显然就上图的AOE网而言，开始→发动机完成→部件集中到位→组装完成就是关键路径，路径长度为5.5。

关键路径算法原理

也就是说，我们只需要找到所有活动的最早开始时间和最晚开始时间，并且比较它们，如果相等就意味着此活动是关键活动，活动间的路径为关键路径。如果不等，则就不是。
为此，我们需要定义如下几个参数。

1.
事件的最早发生时间etv（earliest time ofvertex）：即顶点vk的最早发生时间。
2.
事件的最晚发生时间ltv（latest time ofvertex）：即顶点vk的最晚发生时间，也就是每个顶点对应的事件最晚需要开始的时间，超出此时间将会延误整个工期。
3.
活动的最早开工时间ete（earliest time ofedge）：即弧ak的最早发生时间。
4.
活动的最晚开工时间lte（latest time ofedge）：即弧ak的最晚发生时间，也就是不推迟工期的最晚开工时间。

我们是由1和2可以求得3和4，然后再根据ete[k]是否与lte[k]相等来判断ak是否是关键活动。

关键路径算法

我们将之前的AOE网转化为邻接表结构如图所示，注意与拓扑排序时邻接表结构不同的地方在于，这里弧链表增加了weight域，用来存储弧的权值。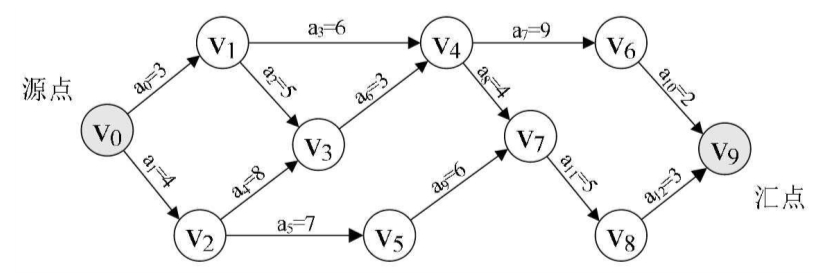


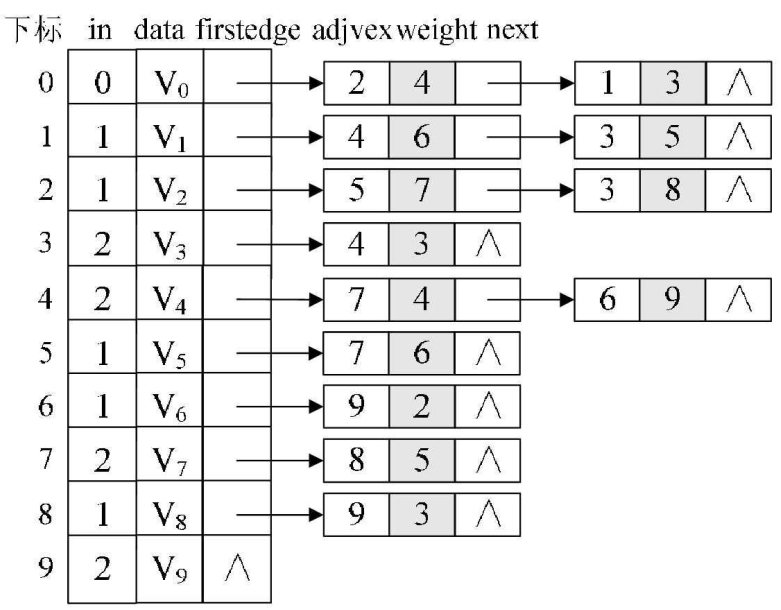
求事件的最早发生时间etv的过程，就是我们从头至尾找拓扑序列的过程，因此，在求关键路径之前，需要先调用一次拓扑序列算法的代码来计算etv和拓扑序列列表。
为此，我们首先在程序开始处声明几个全局变量。

1
2
3
int  *etv,  *ltv;        /*  事件最早发生时间和最迟发生时间数组  */
int  *stack2;            /*  用于存储拓扑序列的栈  */
int  top2;               /*  用于stack2的指针  */

其中stack2用来存储拓扑序列，以便后面求关键路径时使用。
下面是改进过的求拓扑序列算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
/*  拓扑排序，用于关键路径计算  */
Status  TopologicalSort(GraphAdjList  GL)
{
	EdgeNode  *e;
	int  i,  k,  gettop;
	/*  用于栈指针下标  */
	int  top  =  0;                                                                                 
	/*  用于统计输出顶点的个数  */
	int  count  =  0;                                                                               
	/*  建栈将入度为0的顶点入栈  */
	int  *stack;                                                                                    
	stack  =  (int  *)malloc(GL->numVertexes  *  sizeof(int));

	for  (i  =  0;  i  <  GL->numVertexes;  i++)
	{
		if  (0  ==  GL->adjList[i].in)
		{
			stack[++top]  =  i;
		}
	}
	/*  初始化为0  */
	top2  =  0;                                                                                     
	/*  事件最早发生时间  */
	etv  =  (int  *)malloc(GL->numVertexes  *  sizeof(int));              
	for  (i  =  0;  i  <  GL->numVertexes;  i++)
	{
		/*  初始化为0  */
		etv[i]  =  0;
	}                                                                                      
	/*  初始化  */
	stack2  =  (int  *)malloc(GL->numVertexes  *  sizeof(int));
	while  (top  !=  0)
	{
		gettop  =  stack[top--];
		count++;
		/*  将弹出的顶点序号压入拓扑序列的栈  */
		stack2[++top2]  =  gettop;                                                            
		for  (e  =  GL->adjList[gettop].firstedge;  e;  e  =  e->next)
		{
			k  =  e->adjvex;
			if  (!(--GL->adjList[k].in))
			{
				stack[++top]  =  k;
			}
			/*  求各顶点事件最早发生时间值  */
			if  ((etv[gettop]  +  e->weight)  >  etv[k])                      
			{
				etv[k]  =  etv[gettop]  +  e->weight;
			}
		}
	}

	if  (count  <  GL->numVertexes)
	{
		return  ERROR;
	}
	else
	{
		return  OK;
	}
}

第11～15行为初始化全局变量etv数组、top2和stack2的过程。

第21行就是将本是要输出的拓扑序列压入全局栈stack2中。

第27～28行很关键，它是求etv数组的每一个元素的值。

比如说，假如我们已经求得顶点v0对应的etv[0]=0，顶点v1对应的etv[1]=3，顶点v2对应的etv[2]=4，现在我们需要求顶点v3对应的etv[3]，其实就是求etv[1]+len<v1,v3>与etv[2]+len<v2,v3>的较大值。显然3+5<4+8，得到etv[3]=12，如下图所示。在代码中e->weight就是当前弧的长度。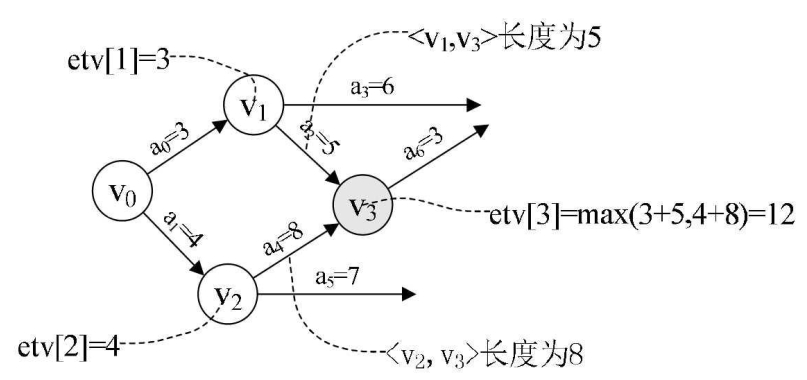

由此我们也可以得出计算顶点vk即求etv[k]的最早发生时间的公式是：
其中P[K]表示所有到达顶点vk的弧的集合。比如上图的P[3]就是<v1,v3>和<v2,v3>两条弧。len<vi,vk>是弧<vi,vk>上的权值。
下面我们来看求关键路径的算法代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
/*  求关键路径，GL为有向网，输出GL的各项关键活动  */
void  CriticalPath(GraphAdjList  GL)
{
	EdgeNode  *e;
	int  i,  gettop,  k,  j;
	/*  声明活动最早发生时间和最迟发生时间变量  */
	int  ete,  lte; 
                                                                                
	/*  求拓扑序列，计算数组etv和stack2的值  */
	TopologicalSort(GL);   
                                                                   
	/*  事件最晚发生时间  */
	ltv  =  (int  *)malloc(GL->numVertexes  *  sizeof(int));        
	for  (i  =  0;  i  <  GL->numVertexes;  i++)
	{
		/*  初始化ltv  */
		ltv[i]  =  etv[GL->numVertexes  -  1];
	}                                  
	/*  计算ltv  */
	while  (top2  !=  0)
	{
		/*  将拓扑序列出栈，后进先出  */
		gettop  =  stack2[top2--];                                                      
		for  (e  =  GL->adjList[gettop].firstedge;  e;  e  =  e->next)
		{                                                                                               
			/*  求各顶点事件的最迟发生时间ltv值  */
			k  =  e->adjvex;
			/*  求各顶点事件最晚发生时间ltv  */
			if  (ltv[k]  -  e->weight  <  ltv[gettop])                    
			{
				ltv[gettop]  =  ltv[k]  -  e->weight;
			}
		}
	}

	/*  求ete，lte和关键活动  */
	for  (j  =  0;  j  <  GL->numVertexes;  j++)                                    
	{
		for  (e  =  GL->adjList[j].firstedge;  e;  e  =  e->next)
		{
			k  =  e->adjvex;          
			/*  活动最早发生时间  */
			ete  =  etv[j];                                                                    
			/*  活动最迟发生时间  */
			lte  =  ltv[k]  -  e->weight;                                            
			/*  两者相等即在关键路径上  */
			if  (ete  ==  lte)                                                                
			{
				printf("<v%d,v%d>  length:  %d  ,  ",GL->adjList[j].data,  GL->adjList[k].data,  e->weight);
			}
		}
	}
}

1．
程序开始执行。第5行，声明了ete和lte两个活动最早最晚发生时间变量。

2．
第6行，调用求拓扑序列的函数。
执行完毕后，全局变量数组etv和栈stack的值如下图所示，top2=10。
也就是说，对于每个事件的最早发生时间，我们已经计算出来了。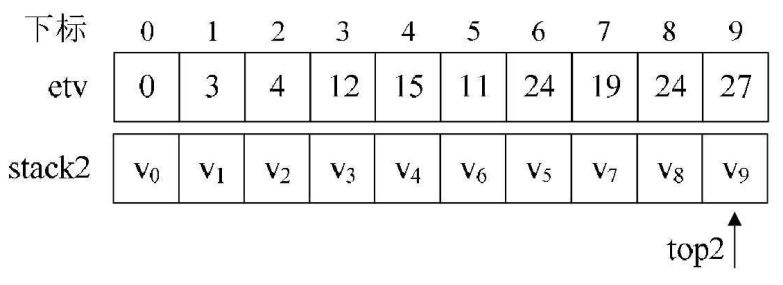

3．
第7～9行为初始化全局变量ltv数组，因为etv[9]=27，所以数组ltv当前的值为：{27,27,27,27,27,27,27,27,27,27}。

4．
第10～19行为计算ltv的循环。
第12行，先将stack2的栈头出栈，由后进先出得到gettop=9。根据邻接表中，v9没有弧表，所以第13～18行循环体未执行。

5．
再次来到第12行，gettop=8，在第13～18行的循环中，v8的弧表只有一条<v8,v9>，第15行得到k=9，因为ltv[9]-3<ltv[8]，所以ltv[8]=ltv[9]-3=24，如图所示。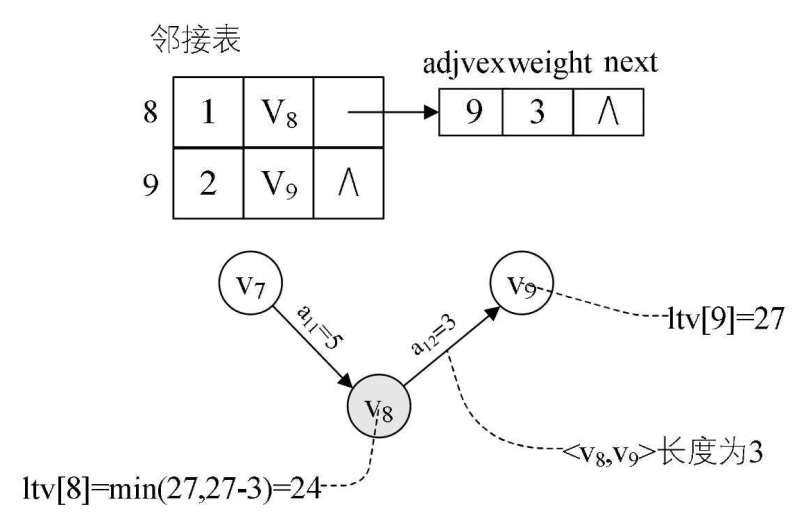

6．
再次循环，当gettop=7、5、6时，同理可算出ltv相对应的值为19、13、25，此时ltv值为：{27，27，27，27，27，13，25，19，24，27}

7．
当gettop=4时，由邻接表可得到v4有两条弧<v4,v6>、<v4,v7>，通过第13～18行的循环，可以得到ltv[4]=min(ltv[7]-4,ltv[6]-9)=min(19-4,25-9)=15，如图所示。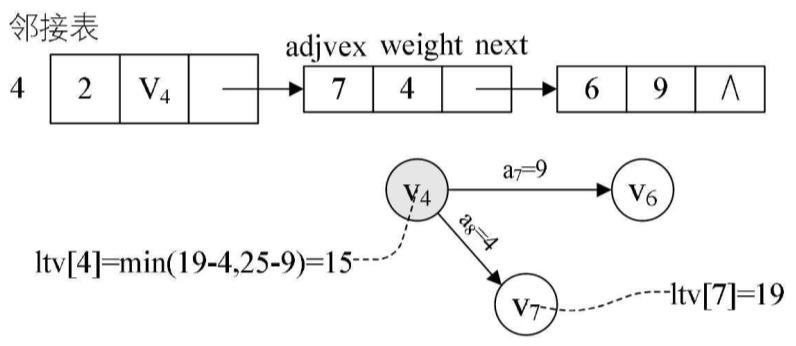

此时你应该发现，我们在计算ltv时，其实是把拓扑序列倒过来进行的。因此我们可以得出计算顶点vk即求ltv[k]的最晚发生时间的公式是：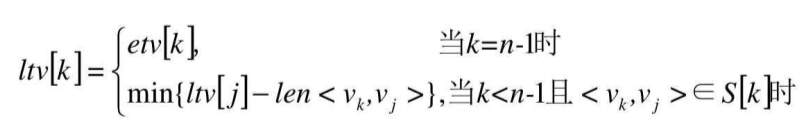

其中S[K]表示所有从顶点vk出发的弧的集合。
比如上图的S[4]就是<v4,v6>和<v4,v7>两条弧，en<vk,vj>是弧<vk,vj>上的权值。
就这样，当程序执行到第20行时，相关变量的值如下图所示，比如etv[1]=3而ltv[1]=7，表示的意思就是如果时间单位是天的话，哪怕v1这个事件在第7天才开始，也可以保证整个工程的按期完成，你可以提前v1事件开始时间，但你最早也只能在第3天开始。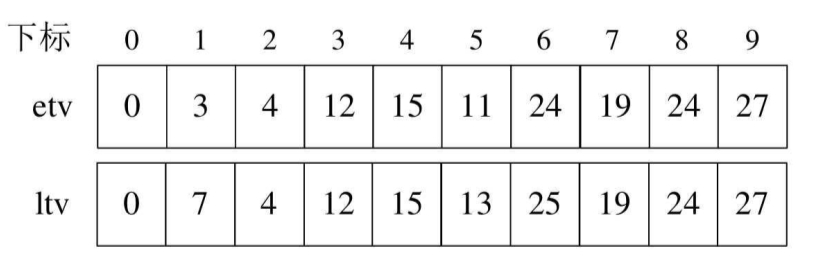

8．
第20～31行是来求另两个变量活动最早开始时间ete和活动最晚开始时间lte，并对相同下标的它们做比较。
两重循环嵌套是对邻接表的顶点和每个顶点的弧表遍历。

9．
当j=0时，从v0点开始，有<v0,v2>和<v0,v1>两条弧。
当k=2时，ete=etv[j]=etv[0]=0。lte=ltv[k]-e->weight=ltv[2]-len<v0,v2>=4-4=0，此时ete=lte，表示弧<v0,v2>是关键活动，因此打印。
当k=1时，ete=etv[j]=etv[0]=0。lte=ltv[k]-e->weight=ltv[1]-len<v0,v1>=7-3=4，此时ete≠lte，因此<v0,v1>并不是关键活动，如图所示。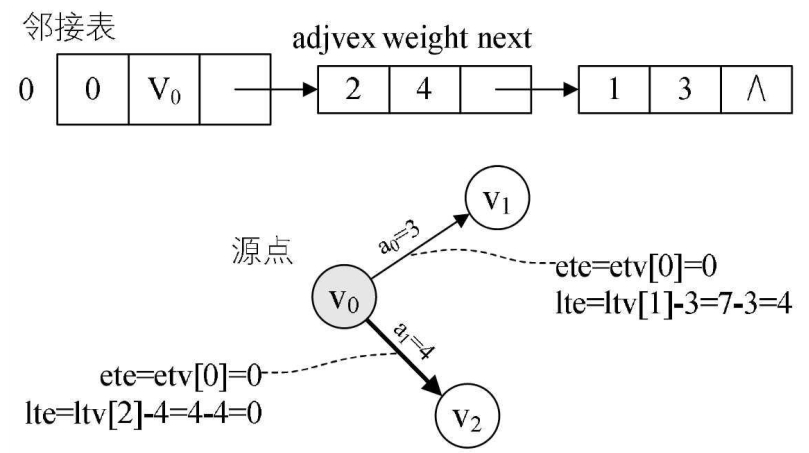

这里需要解释一下，ete本来是表示活动<vk,vj>的最早开工时间，是针对弧来说的。
但只有此弧的弧尾顶点vk的事件发生了，它才可以开始，因此ete=etv[k]。
而lte表示的是活动<vk,vj>的最晚开工时间，但此活动再晚也不能等vj事件发生才开始，而必须要在vj事件之前发生，所以lte=ltv[j]-len<vk,vj>。
所以最终，其实就是判断ete与lte是否相等，相等意味着活动没有任何空闲，是关键活动，否则就不是。

10．
j=1一直到j=9为止，做法是完全相同的，关键路径打印结果为“<v0,v2>4,<v2,v3>8,<v3,v4>3,<v4,v7>4,<v7,v8>5,<v8,v9>3,”，最终关键路径如图所示。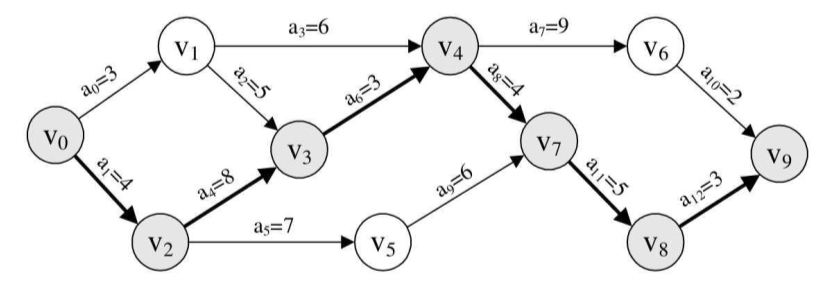

分析整个求关键路径的算法，第6行是拓扑排序，时间复杂度为O(n+e)，第8～9行时间复杂度为O(n)，第10～19行时间复杂度为O(n+e)，第20～31行时间复杂也为O(n+e)，根据我们对时间复杂度的定义，所有的常数系数可以忽略，所以最终求关键路径算法的时间复杂度依然是O(n+e)。

总结回顾

图是计算机科学中非常常用的一类数据结构，有许许多多的计算问题都是用图来定义的。
由于图也是最复杂的数据结构，对它讲解时，涉及到数组、链表、栈、队列、树等之前学的几乎所有数据结构。
因此从某种角度来说，学好了图，基本就等于理解了数据结构这门课的精神。

图的存储结构我们一共讲了五种，如图所示，其中比较重要的是邻接矩阵和邻接表，它们分别代表着边集是用数组还是链表的方式存储。
十字链表是针对有向图邻接表结构的优化，邻接多重表是针对无向图邻接表结构的优化。
边集数组更多考虑的是对边的关注。
用什么存储结构需要具体问题具体分析，通常稠密图，或读存数据较多，结构修改较少的图，用邻接矩阵要更合适，反之则应该考虑邻接表。

图的遍历分为深度和广度两种，各有优缺点，就像人在追求卓越时，是着重深度还是看重广度，总是很难说得清楚。

图的应用是我们这一章浓墨重彩的一部分，一共谈了三种应用：最小生成树、最短路径和有向无环图的应用。

最小生成树，我们讲了两种算法：普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法。普里姆算法像是走一步看一步的思维方式，逐步生成最小生成树。而克鲁斯卡尔算法则更有全局意识，直接从图中最短权值的边入手，找寻最后的答案。

最短路径的现实应用非常多，我们也介绍了两种算法。迪杰斯特拉（Dijkstra）算法更强调单源顶点查找路径的方式，比较符合我们正常的思路，容易理解原理，但算法代码相对复杂。而弗洛伊德（Floyd）算法则完全抛开了单点的局限思维方式，巧妙地应用矩阵的变换，用最清爽的代码实现了多顶点间最短路径求解的方案，原理理解有难度，但算法编写很简洁。

有向无环图时常应用于工程规划中，对于整个工程或系统来说，我们一方面关心的是工程能否顺利进行的问题，通过拓扑排序的方式，我们可以有效地分析出一个有向图是否存在环，如果不存在，那它的拓扑序列是什么？另一方面关心的是整个工程完成所必须的最短时间问题，利用求关键路径的算法，可以得到最短完成工程的工期以及关键的活动有哪些。